Part III- Various Discrete Distributions
Bernoulli Random Variables and Distributions
Binomial Distributions and Sampling with Replacement
Poisson Approximation to the Binomial
A Table of Discrete Distributions
A Bernoulli random variable is one that has only two values, 0 and 1. Often these values are used to encode the outcomes of an experiment which results in one of two mutually exclusive outcomes, for example, the toss of a coin. As another example, a randomly selected student in a course either passes it ("success") or does not pass it ("failure"). If we let X = 1 if the student passes and X = 0 if he or she doesn't, X is a Bernoulli random variable. X is the number of successes in the experiment. Bernoulli random variables are also called Bernoulli trials.
If X is a Bernoulli random variable, let θ = P[X = 1]. Then 1 - θ = P[X = 0]. θ is often called the "success probability". The probability mass function for X can be written in compact form as
![]()
The mean of a Bernoulli random variable X is E[X] = θ and its variance is var(X) = θ(1-θ).
Let X1, X2, ..., Xn be independent Bernoulli random variables or trials, all with the same success probability θ. For example, these could be the outcomes of n tosses of a coin, with 1 indicating a head and 0 indicating a tail. The random variable
![]()
is the total number of successes in the n trials. Its distribution is called the binomial distribution with n trials and success probability θ. Its probability mass function is given by
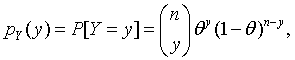
for y = 0, 1, ..., n, where
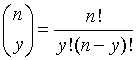
is the binomial coefficient which also appears in the formula for the binomial expansion. The mean of the random variable Y is
![]()
and its variance is
![]()
If a random sample without replacement is taken from a population which is not very large compared to the sample size, the binomial distribution may not be a good approximation. The hypergeometric distribution describes the exact distribution of the number of sample items belonging to the subpopulation of interest. If N is the size of the larger population, M is the size of the subpopulation of interest, n is the size of a sample taken without replacement, and the random variable Y is the number of items in the sample that belong to the subpopulation, then the probability mass function of Y is given by
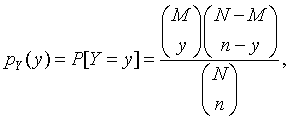
where y is an integer such that 0 ≤ y ≤ M and 0 ≤ n-y ≤ N-M. If we let θ = M/N be the proportion of population members belonging to the subpopulation, then the mean and variance of the hypergeometric random variable are given by
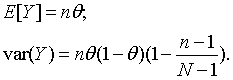
These expressions should be compared to the corresponding expressions for the binomial distribution.
The number of unpredictable natural events of certain types occurring in a time interval of given length is a random variable that is often described by a Poisson distribution. This is especially true of events at an atomic or subatomic level. For example, the number of recorded arrivals at a cosmic ray detector in a one minute time interval is a Poisson random variable. Poisson distributions are important because they are closely related to binomial distributions in certain circumstances.
A Poisson random variable X can have any nonnegative integer value. Its probability mass function is
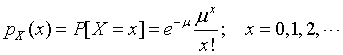
The parameter m is a positive number and is both the mean and the variance of the distribution.
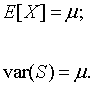
Let Y be a random variable with a binomial distribution based on n trials and with success probability θ. If either nθ2 or n(1-θ)2 is small, the probability mass function of Y can be approximated by the Poisson probability mass function with mean m = nθ. That is to say,
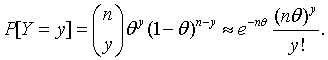
The error of this approximation is no greater than the smaller of the two numbers nθ2 and n(1-θ)2.
Let X1, X2, ... be a sequence of independent Bernoulli random variables, all with the same success probability θ. Let N denote the number of the trial on which the first success occurs. N is a random variable whose value could be any positive integer. For example, an experiment might consist of rolling a standard 6-sided die until the first occurrence of a 2. N would then be the number of rolls required to get a 2, and θ would be 1/6. The distribution of such a random variable is called a geometric distribution with success probability θ. The probability mass function of N is
![]()
The mean and variance of the geometric distribution are given by
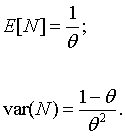
|
Name |
PMF |
Mean |
Variance |
Relationships |
|
|
θ |
θ(1-θ) |
||
|
|
nθ |
nθ(1-θ) |
||
|
|
|
|
||
|
|
μ |
μ |
||
|
|
|
|