


Next: About this document ...
the Institute for Theoretical and Engineering Science
Department of Mathematics
University of Houston
Scientific Computing Seminar
Professor V. Girault
Laboratoire Jacques-Louis Lions , Université Pierre et Marie Curie
A Darcy-Forchheimer model
Thursday, Oct. 26, 2006
3:00 PM- 4:00 PM
Room 634 S&R1
 This is common work with M. Wheeler, I.C.E.S., University of Texas at
Austin.
This is common work with M. Wheeler, I.C.E.S., University of Texas at
Austin.
Abstract:
We consider the steady Darcy-Forchheimer flow of a single-phase fluid
in a porous medium in a two or three dimensional domain 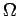 with
boundary
with
boundary
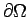 :
:
where 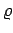 is the density of the fluid,
is the density of the fluid, 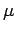 its viscosity,
its viscosity,
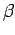 a dynamic viscosity, all assumed to be positive constants,
a dynamic viscosity, all assumed to be positive constants,
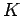 is the permeability tensor, assumed to be uniformly positive
definite and bounded, and
is the permeability tensor, assumed to be uniformly positive
definite and bounded, and 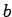 and
and 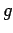 are given functions satisfying
the compatibility condition:
are given functions satisfying
the compatibility condition:
This nonlinear problem is of monotone type. Under mild regularity
assumptions on the data 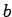 and
and 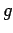 , several authors have proven that
it has a unique weak solution. We propose to solve it numerically
with a finite-element method: discontinuous
, several authors have proven that
it has a unique weak solution. We propose to solve it numerically
with a finite-element method: discontinuous
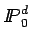 elements for
the velocity
elements for
the velocity
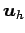 ,
, 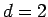 or
or 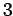 , and discontinuous
, and discontinuous
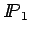 Crouzeix-Raviart elements for the pressure
Crouzeix-Raviart elements for the pressure 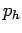 :
:
We prove that this scheme is convergent, again under mild regularity
assumptions on the data, and of order one if the exact solution is
sufficiently smooth. This non-linear scheme can be solved by a convergent alternating-directions algorithm.
 This seminar is easily accessible to persons with disabilities.
For more information or for assistance, please contact the Mathematics
Department at 743-3500.
This seminar is easily accessible to persons with disabilities.
For more information or for assistance, please contact the Mathematics
Department at 743-3500.



Next: About this document ...
Tsorng-Whay Pan
2006-10-12
![]() with
boundary
with
boundary
![]() :
:
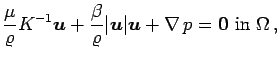
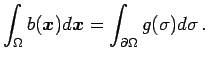
![]() and
and ![]() , several authors have proven that
it has a unique weak solution. We propose to solve it numerically
with a finite-element method: discontinuous
, several authors have proven that
it has a unique weak solution. We propose to solve it numerically
with a finite-element method: discontinuous
![]() elements for
the velocity
elements for
the velocity
![]() ,
, ![]() or
or ![]() , and discontinuous
, and discontinuous
![]() Crouzeix-Raviart elements for the pressure
Crouzeix-Raviart elements for the pressure ![]() :
:
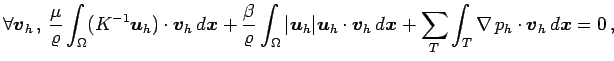
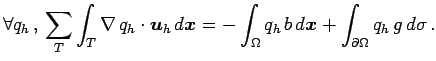
![]() This seminar is easily accessible to persons with disabilities.
For more information or for assistance, please contact the Mathematics
Department at 743-3500.
This seminar is easily accessible to persons with disabilities.
For more information or for assistance, please contact the Mathematics
Department at 743-3500.