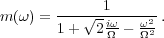
Mathematics of Signal Representations
Math 4355 - Spring 2013 - Homework

Assignment 8, due Thursday, April 4, 2013

1. Consider the Butterworth filter with system function

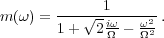
1 m (ω) = 1-+-√2-iω---ω2. Ω Ω2
  1. Verify that it is a Butterworth filter by computing |m(ω)|2.
  2. The impulse response h for this (causal) filter is for t > 0 of the form
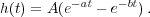
    h(t) = A(e-at - e-bt).
    Determine the (complex) constants A, a and b in terms of Ω.

2. You have obtained the sampled values {f(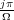jΩπ)}j=-∞∞ for a continuous, square integrable function f which is Ω-bandlimited, Ω > 0.

To process f on your computer, you define a digital “Butterworth convolution” with (any) parameters Ã, a and b,

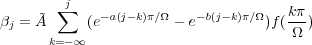
j ˜ ∑ -a(j-k)π∕Ω - b(j- k)π∕Ω kπ- βj = A (e - e )f(Ω ) k=-∞
and reconstruct the corresponding Ω-bandlimited function
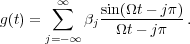
∑∞ sin(Ωt---jπ-) g(t) = βj Ωt- jπ . j=-∞

Compute the system function mΩ of an analog filter L on L2(ℝ) which vanishes outside of the bandlimits,

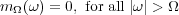
m Ω(ω) = 0, for all |ω| > Ω
and produces the result of the digital convolution with parameters Ã, a, and b,
g = Lf .
Hint: Use the linearity of the sampling series and the properties of the Fourier transform on page 102.

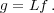
3. If you choose a and b as in the first homework problem, which value of à do you need to obtain that the resulting mΩ satisfies mΩ(0) = 1?

(If you couldn’t compute a and b, state a condition on those two parameters.)