Research Experience for Undergraduates (REU)
Summer 2023
Participants: Sameel Siddiqi and Kevin Sony
Description: Many biological systems that are composed of coupled oscillating elements, such as groups of heart cells and neural tissue, exhibit interesting behavior. For example, the interactions between these oscillating elements allows for traveling and spiral waves to form. When an impurity or defect is present, these systems also support target patterns like the ones shown in the figure below. In this REU, Sameel and Kevin studied the formation of localized target patterns in systems where oscillators are assumed to be globally connected. They used numerical simulations and tools from dynamical systems and partial differential equations to understand how these patterns form.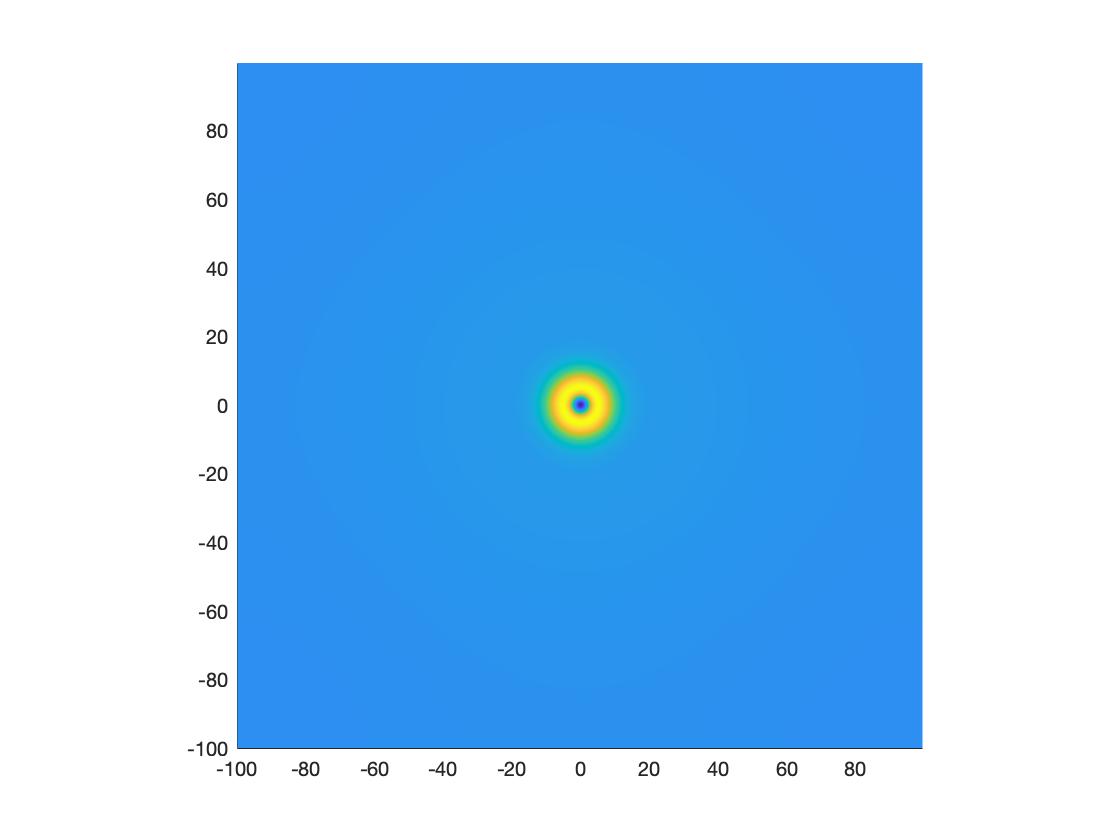
a) 2D Localized Target Pattern
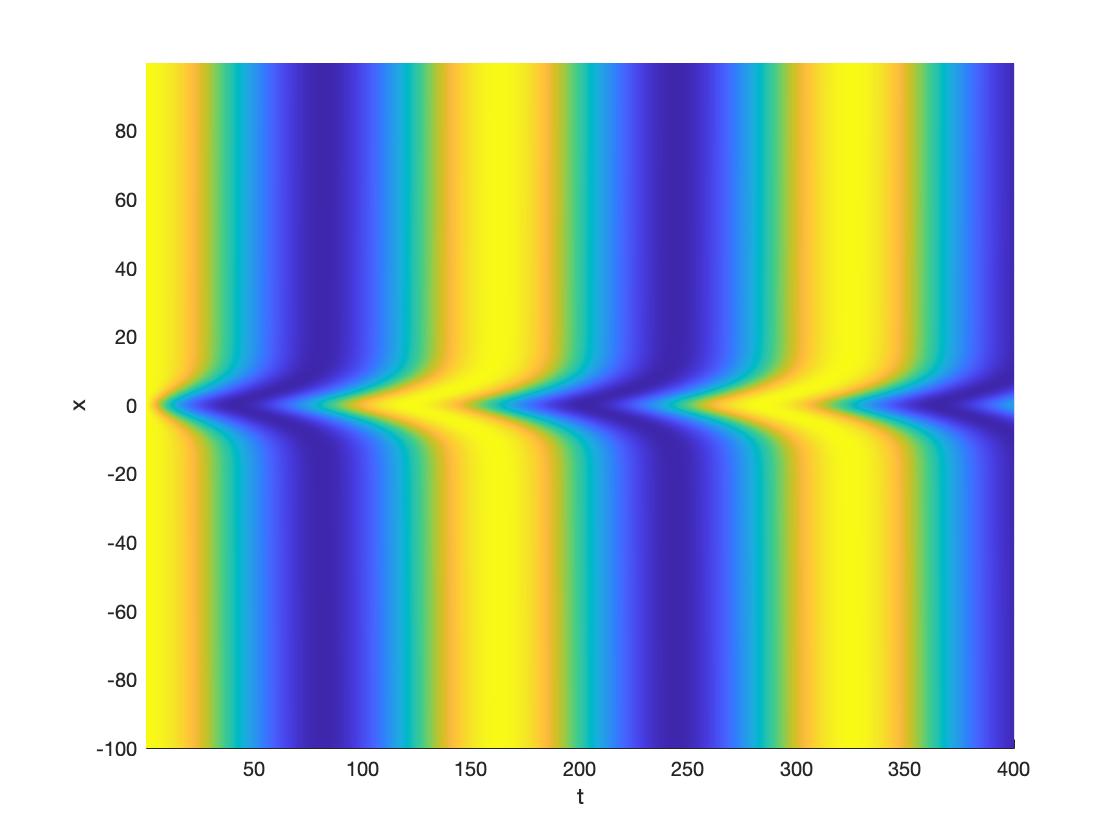
b) Space-time diagram
Summer 2022
Participant: Jared Solomon
Jared studied the formation of spiral chimeras in a nonlocal Fitzhugh-Nagumo system. Using the method of multiple-scales he derived an amplitude equation for this system that is valid close to a Hopf bifurcation. He then further reduced the equations to a phase dynamics approximation. By separating the behavior of solutions near the core from the far field, he identified two different regimes of interest. One which is valid at large scales and follows a viscous eikonal equation (similar to that used when modeling target patterns), and a second regime valid at small scales that exhibits chaotic behavior. This results help elucidate the emergence of chimera states in systems with nonlocal coupling.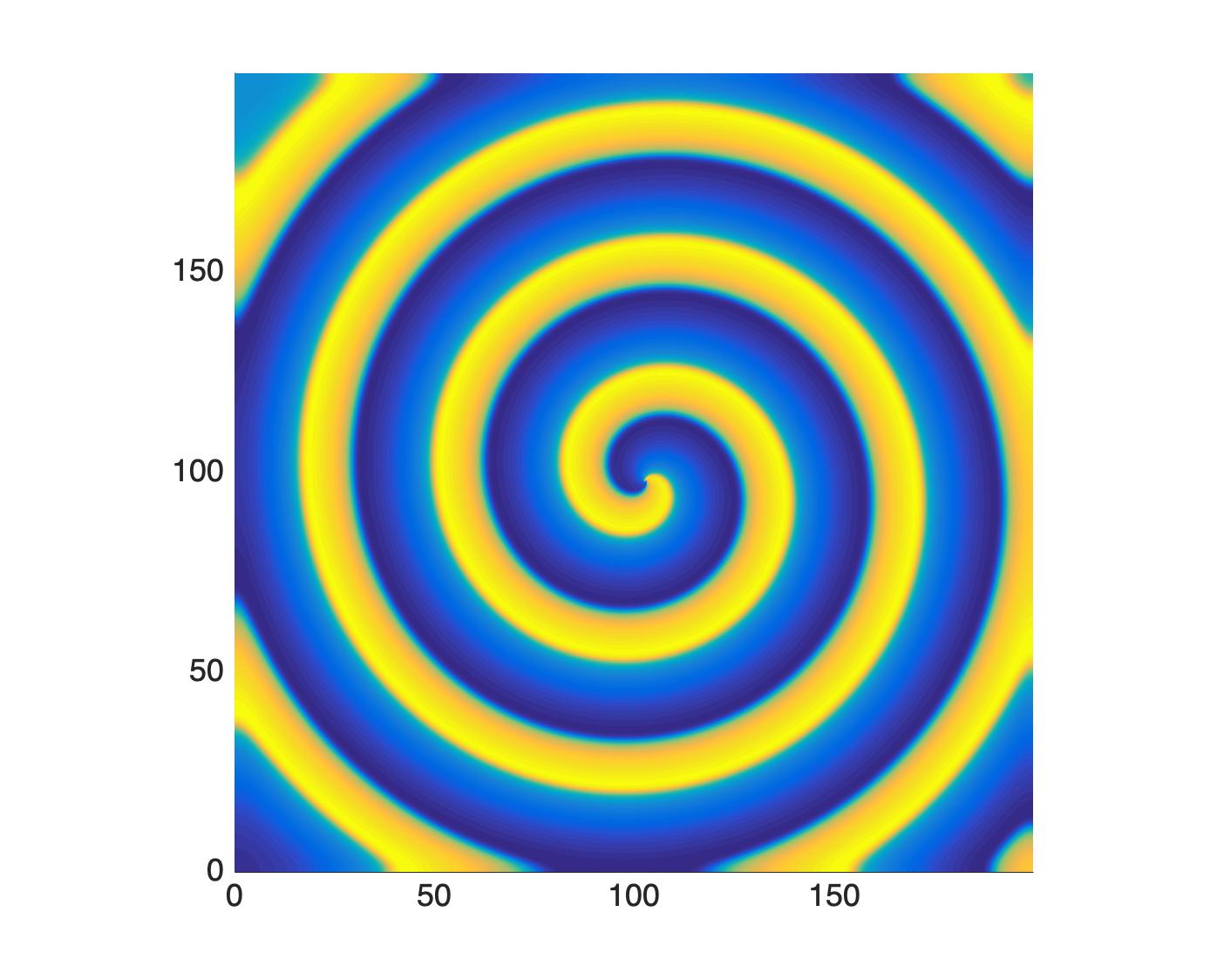
a)Chimera spiral
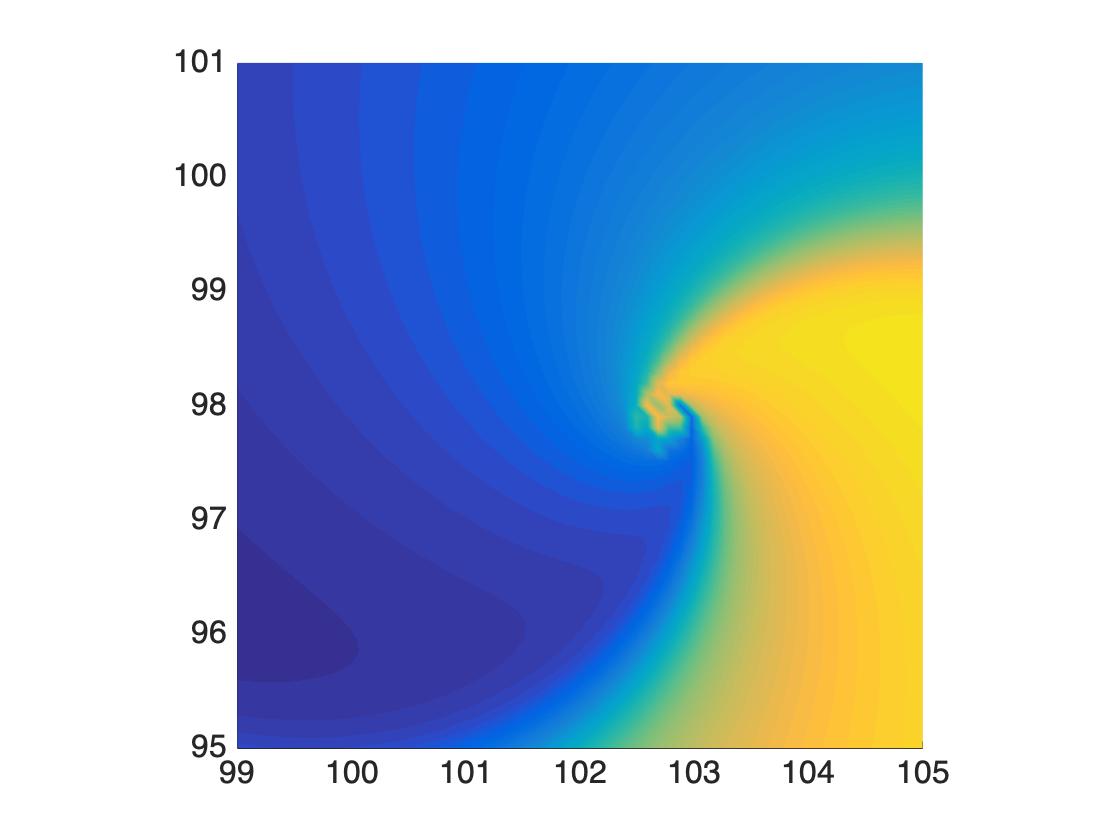
b)Core region
Summer 2021
Participants: Daisy Gomez, Michelle Tran, Artin Seifzadeh
This REU focused on the formation of spiral waves in reaction diffusion systems and the different mechanisms that are used to control their movement. We studied the case when the average concentration of one of the chemical species is used to generate a feedback loop that results in a form of periodic forcing. Depending on the frequency of the forcing term one can then create spiral drift. We then investigated what happens when this feedback is based instead on a weighted average, and looked at two different methods for numerically computing this quantity. One using an exponentially decaying convolution kernel, and another method that used the arc length of the spiral to approximate the average concentration of the chemical inside different concentric circle. We found that in both cases the feedback mechanism is equivalent to adding a periodic forcing to the system, but that in the second case the forcing is given by a piecewise continuous function. See the figure below.To investigate the effects of these control mechanisms we then looked at a dynamical system which models the movement of the spiral's core. The two types of forcing where then used to alter the system's parameter responsible for controlling the drift of the spiral. We found that while a smooth periodic forcing is capable of creating a spiral drift, the piecewise continuous function did not result in straight trajectory.
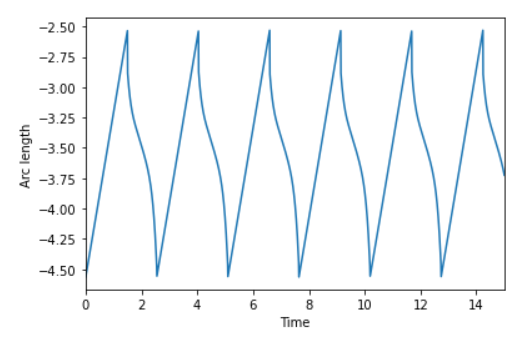
a)
Summer 2020
Participants: Ricardo Del Rio and Shravani Deo
Many biological systems that are composed of coupled oscillating elements, such as groups of heart cells and neural tissue, exhibit interesting behavior. When interactions between these elements is local, traveling and spiral waves form; however, when the coupling is nonlocal new patterns called chimeras states may appear. These novel states consists of regions of synchronous behavior mixed with regions where oscillators act independently of each other.In this project, we used a system of FitzHugh-Nagumo (FHN) equations to study how nonlocal coupling affects pattern formation and the emergence of chimera states. A network of 50 FHN oscillators arranged in a square grid was considered. We found that oscillating spot chimeras and striped chimeras appear depending on the type of coupling used (See poster here).
A second aspect of the project explored the formation of spiral waves in a cellular automaton model. In this model the dynamics of each cell, or oscillator, is governed by a set of rules that take into account the state of the cell itself and its nearest neighbors. Again a square grid of 50 cells was considered. We found that when the number of nearest neighbors that are considered increases the spiral's wavenumber decreases. That is, the spacing between the spiral arms widens (See figures a) b) and c) below).

a)R=1

b)R=3

c)R=5