Editors: D. Bao (San Francisco, SFSU), D. Blecher
(Houston), B. G. Bodmann (Houston), H. Brezis (Paris and Rutgers),
B. Dacorogna (Lausanne), M. Dugas (Baylor), M.
Gehrke (LIAFA, Paris7), C. Hagopian (Sacramento), R. M. Hardt (Rice), S. Harvey (Rice), A. Haynes (Houston), Y. Hattori
(Matsue, Shimane), W. B. Johnson (College Station), M. Rojas (College Station),
Min Ru (Houston), S.W. Semmes (Rice), D. Werner (FU Berlin).
Managing Editors: B. G. Bodmann and K. Kaiser (Houston)
Houston Journal of Mathematics
Contents
T. Tamizh Chelvam Department of Mathematics, Manonmaniam Sundaranar
University, Tirunelveli 627 012, Tamil Nadu, India, ORCID:0000-0002-1878-7847
(tamche59@gmail.com), S. Anukumar Kathirvel, Department of Mathematics,
Manonmaniam Sundaranar University, Tirunelveli 627 012, Tamil Nadu, India
(anukumarsjc@gmail.com), and M. Balamurugan Department of Mathematics, K.R.
College of Arts and Science, Kovilpatti 628503, Tamil Nadu, India (bm4050@gmail.com)
Intersection graph of gamma sets in generalized Cayley graphs of finite rings, pp.
561–582
ABSTRACT. Let R be a finite commutative ring with nonzero identity and U(R) be the
set of all units in R. The graph Γ corresponding to R is the simple undirected graph with
vertex set R in which two distinct vertices x and y are adjacent if and only if
there exists a unit element u in U(R) such that x + uy is a unit in R. First, we
obtain the domination number γ of Γ and characterize all γ-sets in Γ. Using this,
we study about the intersection graph of γ-sets in Γ. The intersection graph
IΓ(R) of gamma sets in Γ is the simple undirected graph with vertex set as the
collection of all γ-sets in Γ and two distinct gamma sets A and B of Γ are
adjacent in IΓ(R) if and only if A ∩ B≠∅. In this paper, first we study about
the degree of vertices in IΓ(R) for all finite commutative rings and prove that
diam(IΓ(R)) ∈{2,∞} and gr(IΓ(R)) ∈{3,4,∞}. Also we obtain a characterization
for IΓ(R) to be connected or Eulerian or unicyclic or split or perfect. At last,
we obtain all finite commutative rings R for which IΓ(R) is either planar or
toroidal.
Weichuan Lin Department of Mathematics, Fujian Normal University, Fuzhou 350007,
Fujian Province, P.R. China (lin@math.is.tohoku.ac.jp, sxlwc936@fjnu.edu.cn) and
Kazuya Tohge College of Science and Engineering, Kanazawa University,
Kakuma-machi, 920-1192, Japan (tohge@se.kanazawa-u.ac.jp)
Periodicity of meromorphic functions and partial sharing values, pp. 583–610
ABSTRACT. We prove two periodicity theorems of a non-constant meromorphic
function sharing 3 or 4 values partially with its shift. Moreover, some examples are given
to illustrate that the assumptions are sharp and necessary.
Qinghua Jiang School of Mathematics and Information Science, Guangzhou University,
Guangzhou, 510006, P. R. China (mathqhjiang@163.com).
Normality of log-harmonic mappings, pp. 611-625
ABSTRACT. This paper concerns the concept of normal log-harmonic mappings of the
form
|
|
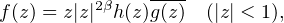from the unit disk D to the complex plane ℂ, where h and g are analytic in the unit disk,
g(0) = 1 and Re{β} > -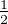
. Furthermore, we obtain some necessary conditions for a
function to be normal.
Ji Guo Institute of Mathematics, Academia Sinica, 6F, Astronomy-Mathematics Building,
No. 1, Sec. 4, Roosevelt Road, Taipei 10617, Taiwan (jiguo@gate.sinica.edu.tw).
Quotient problem for entire functions with moving targets, pp. 627–650
ABSTRACT. As an analogue of the Hadamard quotient problem in number theory, the
quotient problem (in the sense of complex entire functions) for two sequences of entire
functions has recently been solved by Guo. In this paper, we consider the generalization
of this problem in which we allow the coefficients to be entire functions of small growth
by modifying the second main theorem with moving targets to a truncated version. We
also compare our result to a special case in exponential polynomials first studied by
Ritt.
Armando Corro Instituto de Matemática e Estatística, Universidade Federal de
Goiás - UFG, 74690-900, Goiânia, GO, Brazil (corro@ufg.br), Marcelo Souza Instituto
de Matemática e Estatística, Universidade Federal de Goiás - UFG, 74690-900, Goiânia,
GO, Brazil (msouza@ufg.br), and Romildo Pina Instituto de Matemática e
Estatística, Universidade Federal de Goiás - UFG, 74690-900, Goiânia, GO, Brazil
(romildo@ufg.br)
Classes of Weingarten surfaces in S2 × ℝ, pp. 651–664
ABSTRACT. In this study, we explore surfaces in radial conformally flat 3-spaces. We
characterize some specific surfaces of rotation with constant Gaussian and extrinsic
curvatures in these radial 3-spaces. We obtain a special conformal space that is isometric
to S2 × ℝ. We denote this space by M3 and refer to it as the radial model of S2 × ℝ.
We study two classes of Weingarten surfaces in M3. The first class satisfies
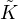E + 
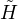2 -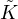
= 0, where 
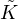is the Gaussian curvature, 
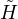is the mean curvature, and
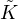E is the extrinsic curvature. We prove that each surface S of this class in M3
corresponds to a minimal surface in ℝ3 or S corresponds to the inversion of a minimal
surface in ℝ3. The second class satisfies 2
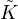E -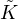
= 0, and we prove that each
surface in this class in M3 corresponds to the EDSGW-surfaces (i.e., surfaces X
satisfying the relation 2⟨X,N⟩H + ⟨X,X⟩K = 0, where N is the unit normal
of X) in the Euclidean space ℝ3. Consequently, each of these two classes of
surfaces has a Weierstrass-type representation depending on two holomorphic
functions.
Ewa Kozłowska-Walania Institute of Mathematics, Faculty of Mathematics, Physics
and Informatics, University of Gdańsk, Wita Stwosza 57, 80-952 Gdańsk, Poland
(retrakt@mat.ug.edu.pl)
Real equations for Riemann surfaces admitting an extremal configuration of three
symmetries, pp. 665–679
ABSTRACT. We consider all the Riemann surfaces with an extremal configuration of
three symmetries, that is the ones with the maximal total number of ovals, being 2g + 4
for g odd and 2g + 3 for g even. It is known that in such a case the symmetries commute.
We find all the corresponding equations for the underlying complex algebraic curve and
its real forms.
Juan de Dios Pérez Juan de Dios Pérez Departamento de Geometría y Topología,
Universidad de Granada, 18071, Granada, Spain (jdperez@ugr.es), Doo Hyun Hwang
Department of Mathematics and RIRCM, Kyungpook National University, Daegu,
41566, Korea (engus0322@knu.ac.kr), and Young Jin Suh Department of
Mathematics and RIRCM, Kyungpook National University, Daegu, 41566, Korea
(yjsuh@knu.ac.kr)
Hypersurfaces in complex Grassmannians whose geodesics are circles and straight lines,
pp. 681–693
ABSTRACT. In this paper we give a new geometric characterization of real
hypersurfaces of type (A) in a complex two-plane Grassmannian G2(ℂm+2), that is, a
tube over a totally geodesic G2(ℂm+1) in G2(ℂm+2) by observing geodesics which are
circles or straight lines in G2(ℂm+2).
Jia Xie School of Mathematics and Information Science, Guangzhou University,
Guangzhou 510006, China. (zyb-may@qq.com), Yongyi Gu Big data and Educational
Statistics Application Laboratory, Guangdong University of Finance and Economics,
Guangzhou 510320, China. (gdguyongyi@163.com), and Wenjun Yuan School of
Mathematics and Information Science, Guangzhou University, Guangzhou 510006,
China. (Corresponding author: wjyuan1957@126.com)
Entire solutions of a certain type of nonlinear differential equations, pp. 695–703
ABSTRACT. In this paper, we study the entire solutions of the differential equations
was considered by Li. Moreover, we use another method to improve some results of Chen
and Gao, whose condition “finite order” can be omitted.
Richard Lechner Institute of Analysis, Johannes Kepler University Linz, Altenberger
Strasse 69, A-4040 Linz, Austria (Richard.Lechner@jku.at)
Direct sums of finite dimensional SLn∞ spaces, pp. 705–745
ABSTRACT. SL∞ denotes the space of functions whose square function is in L∞, and
the subspaces SLn∞, n ∈ ℕ, are the finite dimensional building blocks of SL∞. We show
that the identity operator IdSLn∞ on SLn∞ well factors through operators
T : SLN∞→ SLN∞ having large diagonal with respect to the standard Haar system.
Moreover, we prove that IdSLn∞ well factors either through any given operator
T : SLN∞→ SLN∞, or through IdSLN∞- T. Let X(r) denote the direct sum
∑
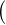n∈ℕ0SLn∞
r, where 1 ≤ r ≤∞. Using Bourgain’s localization method, we obtain
from the finite dimensional factorization result that for each 1 ≤ r ≤∞, the identity
operator IdX(r) on X(r) factors either through any given operator T : X(r) → X(r), or
through IdX(r) - T. Consequently, the spaces 
∑
n∈ℕ0SLn∞
r, 1 ≤ r ≤∞ are all
primary.
Bernhard Burgstaller Departamento de Matematica, Universidade Federal de Santa
Catarina, CEP 88.040-900 Florianópolis-SC, Brasil (bernhardburgstaller@yahoo.de)
A note on a certain Baum–Connes map for inverse semigroups, pp. 747–769
ABSTRACT. Let G denote a countable inverse semigroup. We construct a kind of
a Baum–Connes map K(Ã ⋊ G) → K(A ⋊ G) by a categorial approach via
localization of triangulated categories, developed by R. Meyer and R. Nest
for groups G. We allow the coefficient algebras A to be in a special class of
algebras called fibered G-algebras. This note continues and fixes our preprint
“Attempts to define a Baum–Connes map via localization of categories for inverse
semigroups”.
Shuo Zhang School of Mathematical Sciences, Shanghai Jiao Tong University, 800 Dong
Chuan Road, Shanghai, 200240, P.R. China. (zs.math@sjtu.edu.cn)
Lp-norm estimate for the Bergman projections, pp. 771–796
ABSTRACT. We study the Lp-norm estimates for the Bergman projection
operators on several types of generalized Hartogs triangles in this note. As
a direct application of our main results, we obtain the asymptotic behaviors
for the Lp-norm of the Bergman projections when p tends to the endpoints of
the range of p in which the Bergman projection operators are bounded on Lp
spaces.
S. Berhanu Department of Mathematics, Temple University, Philadelphia, PA 19122,
USA (berhanu@temple.edu) and Jemal Yesuf Department of Mathematics, Addis
Ababa University, Ethiopia (jemalyesuf@su.edu.et)
Continuity of a class of FBI transforms on Sobolev spaces, pp. 797–808
ABSTRACT. We show that a subclass of the generalized FBI transforms that were
introduced in prior work are bounded on Sobolev spaces.
V.V. Tkachuk, Departamento de Matemáticas, Universidad
Autónoma Metropolitana, Av. San Rafael Atlixco, 186, Col. Vicentina, Iztapalapa C.P.
09340, Mexico City, Mexico. Current address: 221 Parker Hall, Department of
Mathematics and Statistics, Auburn University, Auburn, AL, 36849 U.S.A.
(vova@xanum.uam.mx)
The extent of a weakly exponentially separable space can be arbitrarily large, pp.
809–819
ABSTRACT. We prove that a weakly exponentially separable space has extent not
exceeding 𝔠 if it is either normal or first countable. Any metalindelöf weakly
exponentially separable space must be Lindelöf. Besides, for any infinite cardinal κ, there
exists a weakly exponentially separable space X with ext(X) = κ; this result solves a
published open question.
Norberto Ordoñez Universidad Autónoma del Estado de México, Facultad de
Ciencias, Instituto Literario No. 100, Col. Centro, Toluca, Estado de México, C. P.
50000, MÉXICO (nordonezr@uaemex.mx)
The hyperspace of meager subcontinua, pp. 821–834
ABSTRACT. Given a metric continuum X, we define the hyperspace of meager
subcontinua of X, denoted by M(X), as the collection of all subcontinua of X with empty
interior. In this paper we study the connectedness, compactness, arcwise connectedness
and contractibility of this hyperspace. As a main result we obtain that for a
smooth dendroid X the hyperspace M(X) is contractible. Also we raise open
problems.
B. D. Daniel Lamar University, Department of Mathematics, Beaumont, Texas
77710-0047 (dale.daniel@lamar.edu) and M. Tuncali Nipissing University,
Department of Computer Science and Mathematics, North Bay, Ontario P1B 8L7
(muratt@nipissingu.ca)
Metrizability of products in compacta in which each continuum of convergence is
metrizable, pp. 835–843
ABSTRACT. Treybig showed that if the product of two infinite compacta is the image
of some compact ordered space then each factor of the product must be metrizable.
Treybig’s theorem motivates the study of those conditions under which a space admits
products with only metric components. Somewhat later, the second-named author
extended this result to continua satisfying various rim properties. A natural condition to
impose on such spaces is that the space have the property that each continuum of
convergence is metrizable. Herein, we give some product theorems in such spaces.