HOUSTON JOURNAL OF MATHEMATICS

 Expected Edition Vol. 49, No. 4, 2023

Editors:  D. Bao (San Francisco, SFSU), S. Berhanu (Temple), D. Blecher (Houston), B. G. Bodmann (Houston), H. Brezis (Paris and Rutgers), B.  Dacorogna (Lausanne), M. Gehrke (LIAFA, Paris7), R. M. Hardt (Rice), S. Harvey (Rice), A. Haynes (Houston), Y. Hattori (Matsue, Shimane), W. B. Johnson (College Station), H. Koivusalo (Bristol), M. Marsh (Sacramento), M. Rojas (College Station), Min Ru (Houston), S.W. Semmes (Rice), D. Werner (FU Berlin).
Managing Editors: B. G. Bodmann and A. Haynes (Houston)

 Houston Journal of Mathematics

Contents

Zhidong Pan, Department of Mathematics, Saginaw Valley State University, University Center, MI 48710, USA (pan@svsu.edu).
Filters, separating vectors, and algebraic reflexivity of scaling covers, pp. 715–739.

ABSTRACT. We introduce the concept of scaling covers of operators, which generalizes various notions of operator orbits. Necessary and sufficient conditions are given for scaling covers to be algebraically reflexive, which generalize several results in the literature. A novelty in our approach in this paper is to create two filters as tools to help us capture separating vectors. Among interesting connections, we show that invariants of Möbius transformations can be used to construct nontrivial reflexive scaling covers. We also characterize the algebraic reflexive covers of a family of scalar-stable sets of operators on a 2-dimensional Hilbert space.  

Jireh Loreaux, Department of Mathematics and Statistics, Southern Illinois University Edwards-ville, 1 Hairpin Dr., Edwardsville, IL 62026-1653, USA (jloreau@siue.edu), P. W. Ng, Department of Mathematics, University of Louisiana at Lafayette, 217 Maxim Doucet Hall, P. O. Box 43568, Lafayette, Louisiana 70504–3568, USA (png@louisiana.edu), and Arindam Sutradhar, Department of Mathematics, Indian Institute of Technology Madras, 5th Floor, NAC, NAC Road, Chennai, Tamil Nadu 600036, India (arindam1050@gmail.com).
Essential codimension and lifting projections, pp. 741–783.

ABSTRACT. We consider extensions of Brown–Douglas–Fillmore’s notion of essential codimension to pairs of projections in the multiplier algebra of a separable stable C*-algebra ℬ whose difference lies in the canonical ideal ℬ. We investigate both a concrete definition akin to the original one given by Brown–Douglas–Fillmore, as well as a KK-theoretic definition, and show that they coincide. We explore the properties as well as an axiomatization of essential codimension.

Using essential codimension, we establish K-theoretic necessary and sufficient conditions for projection lifting from certain corona algebras (whose canonical ideals need not have real rank zero).

Huibo Ma, School of Mathematical Sciences, Capital Normal University, Beijing, 100048, China (m18843409168@163.com), Yihong Hao, School of Mathematics, Northwest University, Xi’an, 710127, China (haoyihong@126.com), and Xiaoliang Cheng, College of Mathematics and Computer, Jilin Normal University, Siping, 136000, China (chengxiaoliang92@163.com).
Submanifolds of Hua domains and the complex Euclidean space, pp. 785–794.

ABSTRACT. By proving a new contradictory equation on Nash functions, we study the existence of the common Kähler submanifold between the complex Euclidean space and the Hua domains equipped with their Bergman metrics. In particular, our result is a generalization and complement of known results obtained by Zhang-Ji in [29].  

Young Jin Suh, Department of Mathematics and RIRCM, Kyungpook National University, Daegu 41566, Republic of Korea (yjsuh@knu.ac.kr).
Yamabe and gradient Yamabe solitons on real hypersurfaces in the complex two-plane Grassmannians, pp. 795–820.

ABSTRACT. In this paper, we give a complete classification of Yamabe solitons and gradient Yamabe solitons on real hypersurfaces in the complex two-plane Grassmannian G₂(ℂ^m+2). Next as an application we show a complete classification of quasi-Yamabe and gradient quasi-Yamabe solitons on real hypersurfaces in the complex two-plane Grassmannian G₂(ℂ^m+2).  

Yingcui Zhao, School of Computing, Dongguan University of Technology, No.1 Daxue Road, Dongguan City, 523808, Guangdong Province, China (zycchaos@126.com), and Lidong Wang, School of Statistics and Data Science, Zhuhai College of Science and Technology, No.8 Anji East Road, Zhuhai City, 519041, Guangdong Province, China (wld0707@126.com).
Specification-like properties of a set-value map and its inverse limit, pp. 821–832.

ABSTRACT. We consider specification-like properties of a set-valued map and their implications on the associated inverse limit space. (Weak) Specification of a set-valued map and its inverse limit implies each other. Hausdorff metric almost specification of a set-valued map implies almost specification of the generalized inverse limit, and the latter implies almost specification in the sense of orbit of the set-valued map. We end with an example which shows for set-valued map almost specification in the sense of orbit cannot imply Hausdorff metric almost specification.  

Michel L. Lapidus, Department of Mathematics, University of California, Riverside, 900 University Ave, Riverside, 92521, California, USA (lapidus@math.ucr.edu), Machiel van Frankenhuijsen, Department of Mathematics, Utah Valley University, 800 W University Pkwy, Orem, 84058, Utah, USA (vanframa@uvu.edu), and Edward K. Voskanian, Department of Mathematics, Norwich University, 158 Harmon Dr, Northfield, 05663, Vermont, USA (evoskani@norwich.edu).
Diffraction measures and patterns of the complex dimensions of self-similar fractal strings. I. The lattice case, pp. 833–859.

ABSTRACT. We give a generalization of Lagarias’s formula for diffraction by ideal crystals, and we apply it to the lattice case, in preparation for addressing the problem of quasicrystals and complex dimensions posed by Lapidus and van Frankenhuijsen concerning the quasiperiodic properties of the set of complex dimensions of any nonlattice self-similar fractal string. More specifically, in this paper, we consider the case of the complex dimensions of a lattice (rather than of a nonlattice) self-similar string and show that the corresponding diffraction measure exists, is unique, and is given by a suitable continuous analogue of a discrete Dirac comb. We also obtain more general results concerning the autocorrelation measures and diffraction measures of generalized idealized fractals associated to possibly degenerate lattices and the corresponding extension of the Poisson Summation Formula.  

Adam Brown-Sarre, Department of Mathematical and Physical Sciences, La Trobe University, Bendigo 3552, Australia (20356213@students.latrobe.edu.au), Gerardo González Robert, Department of Mathematical and Physical Sciences, La Trobe University, Bendigo 3552, Australia (G.Robert@latrobe.edu.au), and Mumtaz Hussain, Department of Mathematical and Physical Sciences, La Trobe University, Bendigo 3552, Australia (m.hussain@latrobe.edu.au).
Metrical properties of weighted products of consecutive Lüroth digits, pp. 861–897.

ABSTRACT. The Lüroth expansion of a real number x ∈ (0,1] is the series

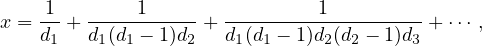
with d_j ∈ ℕ_≥2 for all j ∈ ℕ. Given m ∈ ℕ, t = (t₀,…,t_m−1) ∈ ℝ_>0^m−1 and any function Ψ : ℕ → (1,∞), define

We establish a Lebesgue measure dichotomy statement (a zero-one law) for ℰ_t(Ψ) under a natural non-removable condition liminf _n→∞Ψ(n) >  1. Let B be given by

For any m ∈ ℕ, we compute the Hausdorff dimension of ℰ_t(Ψ) when either B = 1 or B = ∞. We also compute the Hausdorff dimension of ℰ_t(Ψ) when 1 < B < ∞ for m = 2.

Juan Zhao, School of Mathematical Sciences, Dalian University of Technology, Dalian, Liaoning 116024, China (ksc@mail.dlut.edu.cn).
A Nekhoroshev type theorem for nonlinear Schrödinger equation on the d-dimensional torus, pp. 899–919.

ABSTRACT. In this paper, we study the long time dynamical behavior of the solutions for d-dimensional nonlinear Schrödinger equation on the torus 𝕋^d. Precisely, by using Birkhoff normal form technique, we prove the subexponential long time stability of solutions with small initial data in Gevrey space.  

Said El Manouni, College of Science, Department of Mathematics and Statistics, Imam Mohammad Ibn Saud Islamic University (IMSIU), P. O. Box 90950, Riyadh 11623, Saudi Arabia (samanouni@imamu.edu.sa), Kanishka Perera, Department of Mathematical Sciences, Florida Institute of Technology, 150 W University Blvd, Melbourne, FL 32901-6975, USA (kperera@fit.edu), and Patrick Winkert, Technische Universität Berlin, Institut für Mathematik, Straße des 17. Juni 136, 10623 Berlin, Germany (winkert@math.tu-berlin.de).
(p,q)-Laplacian problems with parameters in bounded and unbounded domains, pp. 921–937.

ABSTRACT. The purpose of this paper is to study the existence and nonexistence of nontrivial solutions for quasilinear elliptic problems driven by the nonhomogeneous (p,q)-Laplace operator −Δ_p − Δ_q depending on two parameters in bounded and unbounded domains. First, using variational methods, we prove the existence and nonexistence of positive solutions for a class of sublinear (p,q)-Laplacian problems with two parameters. Second, using a nonstandard variational approach, we prove the existence of bounded solutions for nonlinear problems of (p + q) sublinear type involving the (p,q)-Laplace operator with two parameters in unbounded domains.  

Tom Richmond, Department of Mathematics, Western Kentucky University, Bowling Green, KY 42101, USA (tom.richmond@wku.edu), and Eliza Wajch, Institute of Mathematics, Siedlce University of Natural Sciences and Humanities, 3. Maja 54, 08-110 Siedlce, Poland (eliza.wajch@gmail.com).
A quasi-metrization theorem for hybrid topologies on the real line in ZF, pp. 939–952.

ABSTRACT. Hybrid topologies on the real line have been studied by various authors. Among the hybrid spaces, there are also the Hattori spaces. However, some of the hybrid spaces are not homeomorphic to Hattori spaces. In this article, a common generalization of at least four kinds of the hybrid topologies on the real line is described. In the absence of the Axiom of Choice, a quasi-metrization theorem for such hybrid spaces is proved. It is shown that Kofner’s quasi-metrization theorem for generalized ordered spaces is false in every model of ZF in which there exists an infinite Dedekind-finite subset of the real line.  

A. C. Megaritis, University of Patras, Department of Mathematics, 26504 Patra, Greece (acmegaritis@upatras.gr), and F. Sereti, University of Western Macedonia, Department of Mathematics, 52100 Kastoria, Greece (seretifot@gmail.com).
Almost regular spaces and universal elements, pp. 953–969.

ABSTRACT. The universality problem for classes of topological spaces constructs a research field on Topology, which focuses on finding universal elements or verifying the non-existence of such elements in given classes of spaces. In this paper, we study this problem for classes of almost regular spaces. We prove that the class of all almost regular T₀-spaces of weight less than or equal to an infinite cardinal τ is saturated and thus, we answer positively to this problem showing the existence of universal spaces in this class. Then, based on this main result, we succeed to give more positive answers to the universality problem in various other classes of spaces, proving the existence of corresponding universal spaces.  

Bin Zhao, School of Mathematics and Statistics, Shaanxi Normal University, Xi’an 710119, Shaanxi, P.R. China (zhaobin@snnu.edu.cn), Zhengmao He, School of Mathematics and Statistics, Shaanxi Normal University, Xi’an 710119, Shaanxi, P.R. China (hezhengmao@snnu.edu.cn), and Kaiyun Wang, School of Mathematics and Statistics, Shaanxi Normal University, Xi’an 710119, Shaanxi, P.R. China (wangkaiyun@snnu.edu.cn).
On co-sober spaces, pp. 971–988.

ABSTRACT. In this paper, let 𝒬(P) denote the poset of all nonempty compact saturated subsets of the Scott space of a poset P with the reverse inclusion order. We prove that (1) every zero-dimensional T₀ space is co-sober; (2) for a complete lattice L, if the Scott space on 𝒬(L) is co-sober, then the Scott space on L is co-sober; (3) every locally compact and coherent T₀ space is co-sober. In addition, we introduce the notion of weakly co-sober spaces and discuss some properties of weakly co-sober spaces. Based on weakly co-sober spaces and Scott spaces, we show that if both P and Q are quasicontinuous posets or both of them are complete lattices, then P is order isomorphic to Q iff 𝒬(P) is order isomorphic to 𝒬(Q).