|
Air
Quality
Modeling
Project
Physiological
Fluid
Dynamics
Project
Wavelets
and
Visual
Computing
Project
Symmetry
and
Neuroscience
Project
Einstein
Metrics
Project
Air
Quality
Modeling
Project
 (Amundson,
Fitzgibbon,
Glowinski,
He,
Kuznetsov)}
The
EPA
funded
research
on air
quality
modeling
is aimed
at developing
a performance-portable
multi-scale
air
quality
modeling
system
to simulate
various
chemical
and
physical
processes
that
are
important
for
understanding
atmospheric
trace
gas
transformations
and
distributions.
The
photochemical
model
consists
of a
set
of coupled
partial
differential
equations,
one
for
each
chemical
species.
The
input
of these
equations
is complete
local
weather
data
and
concentrations
of chemical
precursor
molecules,
ideally
determined
by real-time
monitoring.
Many
of the
monitored
species
undergo
chemical
reactions,
decreasing
the
concentration
of one
species,
and
increasing
the
concentration
of another
species
to potentially
harmful
levels.
The
most
advanced
applied
mathematical
techniques
and
massively
parallel
supercomputer
simulations
are
required
to predict
the
future
concentration
of potentially
harmful
species.
The
methods
currently
employed
depend
on the
computational
science
of the
late
1970's
and
early
1980's.
They
do not
utilize
the
dramatic
breakthroughs
of the
last
twenty
years
in the
science
of computation.
Effective
use
of modern
technology,
especially
large-scale
distributed
parallel
computing
and
state
of the
art
computational
methodology,
will
allow
us to
increase
both
the
efficiency
and
speed
of computation.
(Amundson,
Fitzgibbon,
Glowinski,
He,
Kuznetsov)}
The
EPA
funded
research
on air
quality
modeling
is aimed
at developing
a performance-portable
multi-scale
air
quality
modeling
system
to simulate
various
chemical
and
physical
processes
that
are
important
for
understanding
atmospheric
trace
gas
transformations
and
distributions.
The
photochemical
model
consists
of a
set
of coupled
partial
differential
equations,
one
for
each
chemical
species.
The
input
of these
equations
is complete
local
weather
data
and
concentrations
of chemical
precursor
molecules,
ideally
determined
by real-time
monitoring.
Many
of the
monitored
species
undergo
chemical
reactions,
decreasing
the
concentration
of one
species,
and
increasing
the
concentration
of another
species
to potentially
harmful
levels.
The
most
advanced
applied
mathematical
techniques
and
massively
parallel
supercomputer
simulations
are
required
to predict
the
future
concentration
of potentially
harmful
species.
The
methods
currently
employed
depend
on the
computational
science
of the
late
1970's
and
early
1980's.
They
do not
utilize
the
dramatic
breakthroughs
of the
last
twenty
years
in the
science
of computation.
Effective
use
of modern
technology,
especially
large-scale
distributed
parallel
computing
and
state
of the
art
computational
methodology,
will
allow
us to
increase
both
the
efficiency
and
speed
of computation.
Air
Quality
Modeling
is already
organized
around
research,
training,
and
vertical
integration.
Current
participants
include
postdocs
(Basak,
Lubertino,
Yoo),
graduate
students
(Martynenko,
Myers,
Smith,
Wang),
and
undergraduate
students
(Ghere,
Lewis).
The
graduate
students
currently
work
on a
variety
of problems
involving
novel
operator
splitting
techniques
and
stiff
ODE
solvers,
as well
as studies
of various
aspects
of parallel
and
high
performance
computing.
They
present
their
work
as PhD
and
MS thesis
projects
in the
Computational
Sciences
program.
This
program
allows
students
to obtain
a multi-disciplinary
education
across
traditional
departmental
lines.
Through
capstone
senior
research
projects,
the
undergraduate
students
participate
in the
development
of support
tools
for
the
modular
visualization
environment
and
statistical
model
evaluation.
The
group
holds
biweekly
meetings.
Students,
along
with
postdocs
and
faculty,
participate
in three
end-of-semester
review
meetings
(Fall,
Spring,
Summer)
at which
they
present
talks
and
summaries
of research
projects.
This
project
has
two
primary
goals:
a performance-enhanced
multi-scale
air
quality
model
system,
better
able
to exploit
modern
mathematical
algorithms
and
microprocessor-based
parallel
computers,
and
an interdisciplinary
program
on air
quality
modeling.
Physiological
Fluid
Dynamics
Project
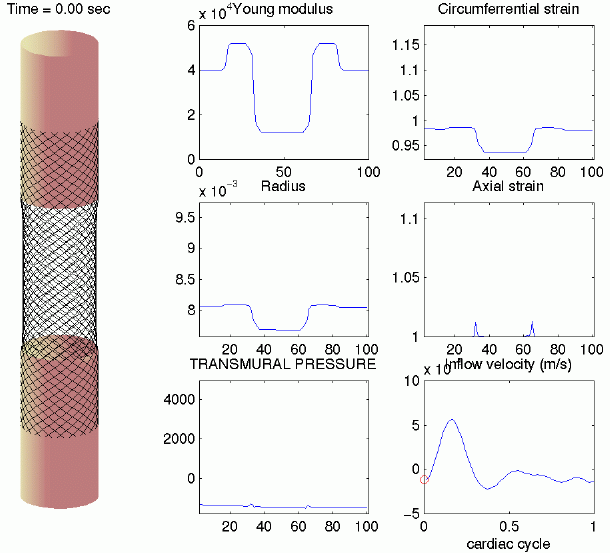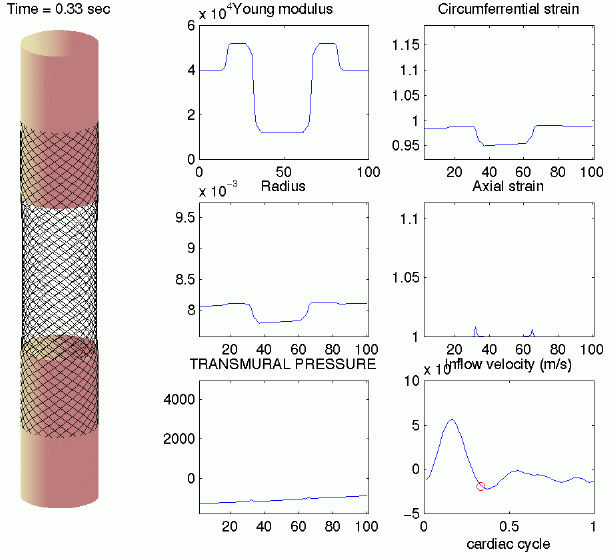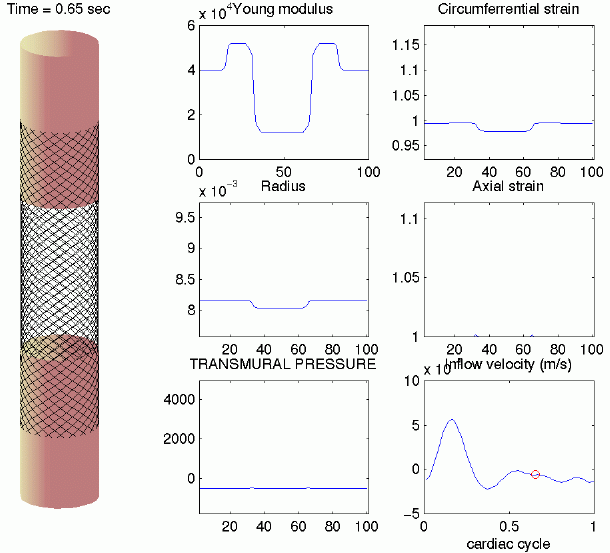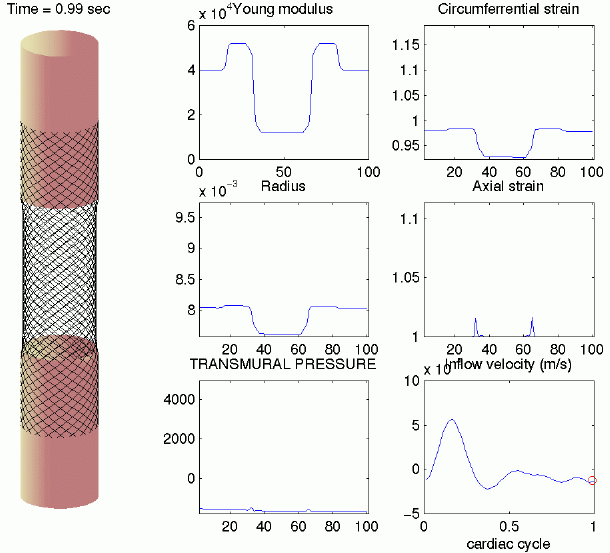 (Canic)
This
is an
interdisciplinary
project
in the
endovascular
treatment
of abdominal
aortic
aneurysms
(AAA)
that
uses
expertise
in the
fields
of cardiovascular
interventions
(Krajcer,
M.D.,
Interventional
Cardiologist
at St.~Luke's
Episcopal
Hospital
and
the
Texas
Heart
Institute),
mechanical
engineering
(Ravi-Chandar,
UT Austin
Center
for
Mechanics
of Solids,
Structures
and
Materials),
computer
science
Mirkovic,
and
applied
mathematics
Canic.
Endovascular
prostheses,
called
stents,
are
used
in the
treatment
of AAA.
There
are
two
principal
objectives:
to carry
out
a quantitative
analysis
of the
(hemodynamics)
equations
that
model
the
performance
of stents,
and
to aid
physicians
in the
choice
of a
stent. (Canic)
This
is an
interdisciplinary
project
in the
endovascular
treatment
of abdominal
aortic
aneurysms
(AAA)
that
uses
expertise
in the
fields
of cardiovascular
interventions
(Krajcer,
M.D.,
Interventional
Cardiologist
at St.~Luke's
Episcopal
Hospital
and
the
Texas
Heart
Institute),
mechanical
engineering
(Ravi-Chandar,
UT Austin
Center
for
Mechanics
of Solids,
Structures
and
Materials),
computer
science
Mirkovic,
and
applied
mathematics
Canic.
Endovascular
prostheses,
called
stents,
are
used
in the
treatment
of AAA.
There
are
two
principal
objectives:
to carry
out
a quantitative
analysis
of the
(hemodynamics)
equations
that
model
the
performance
of stents,
and
to aid
physicians
in the
choice
of a
stent.
A
first
generation
hemodynamics
model
was
developed
to study
blood
flow
through
axisymmetric
elastic
tubes
with
elastic
properties
that
change
discontinuously.
Solving
this
model
requires
a new
mathematical
theory
for
solutions
of quasilinear
hyperbolic
equations
with
discontinuous
coefficients.
The
next
steps
are
the
development
of a
three-dimensional
model,
its
implementation
on advanced
parallel
computer
architecture,
and
its
simulation.
Both
education
and
research
have
been
integrated
into
this
project
from
its
inception.
Three
undergraduate
students
(Pritts,
Burns
in Math;
Roy
in CS)
and
a postdoc
(Kim)
have
worked
on modeling,
numerical
simulation,
and
the
development
of a
theory
to study
the
first
generation
equations.
In Summer
2001,
two
REU
students
also
worked
on thenumerical
analysis
and
simulation
of the
simplified
equations.
Both
students
wrote
papers
that
will
be archived
as Mathematics
Department
preprints.
Two
graduate
students
(Burns
and
Sharma)
will
begin
their
PhD
thesis
work
on this
project
in Fall
2001,
and
a postdoc
(Vassilevski)
will
begin
work
on the
3D hemodynamics
model
in Spring
2001.
Wavelets
and
Visual
Computing
Project
(Papadakis,
Paulsen)
This
project
will
bring
together
researchers
and
students
in the
fields
of functional,
harmonic,
and
wavelet
analysis
with
researchers
in the
fields
of visual
computing
and
signal
processing.
Students
can
integrate
their
mathematical
research
with
projects
on visual
computing
and
signal
processing
under
development
in UH's
Center
for
Bioimaging
and
Biocomputation.
For
example,
Papadakis
is involved
in developing
multiresolution
deformable
models
and
non-separable
multidimensional
multiresolution
designs
in collaboration
with
faculty
in computer
science
(Kakadiaris),
electrical
and
computer
engineering
(Karayiannis),
and
chemistry
(Kouri).
These
designs
are
applied
to low
bit
rate
video
compression,
high
resolution
video
transmissions,
compression
and
progressive
transmission
of images
of surfaces,
geoscientific
data
analysis
and
edge
detection,
and
texture
segmentation.
Paulsen
and
a PhD
student
(Holmes)
are
involved
in more
abstract
research
on frame
theory,
aimed
at classifying
and
generating
frames
with
special
properties
that
should
eventually
have
application
to data
compression.
Student
projects
will
be drawn
from
such
applications
as the
analysis
and
synthesis
of human
motion,
biomedical
imaging
and
geoscientific
data
analysis.
Graduate
students
and
postdocs
will
participate
in the
development
of algorithms
based
on their
research,
while
undergraduates
can
perform
simulations
and
experiments
to test
the
newly
developed
codes.
Symmetry
and
Neuroscience
Project
 (Field,
Golubitsky,
Stewart)
Identical
coupled
systems
of ODE
or {\em
coupled
cell
systems}
are
discrete-space
continuous-time
models
that
have
proved
useful
as models
of locomotor
central
pattern
generators
(animal
gaits)
and
of the
visual
cortex
(geometric
visual
hallucination
patterns).
The
dynamics
of cell
systems
can
be quite
complex
(oscillation,
heteroclinic
cycles,
cycling
chaos),
even
when
there
are
only
a few
cells
and
the
dynamics
within
each
cell
are
simple.
For
example,
the
coupling
of two
one-dimensional
cells
can
produce
oscillation
even
though
neither
one
by itself
can
oscillate.
A central
question
about
coupled
cell
system
dynamics
concerns
the
relative
balance
between
the
internal
dynamics
of each
cell
and
the
way
the
cells
are
coupled.
Coupled
cell
systems
also
have
symmetry
(permutations
of the
cells
that
preserve
the
coupling),
which
often
organizes
much
of the
interesting
dynamics.
The
patterns
of oscillation
that
cell
systems
can
exhibit
depend
solely
on the
architecture
of the
cell
system,
as our
work
on animal
gaits
has
shown. (Field,
Golubitsky,
Stewart)
Identical
coupled
systems
of ODE
or {\em
coupled
cell
systems}
are
discrete-space
continuous-time
models
that
have
proved
useful
as models
of locomotor
central
pattern
generators
(animal
gaits)
and
of the
visual
cortex
(geometric
visual
hallucination
patterns).
The
dynamics
of cell
systems
can
be quite
complex
(oscillation,
heteroclinic
cycles,
cycling
chaos),
even
when
there
are
only
a few
cells
and
the
dynamics
within
each
cell
are
simple.
For
example,
the
coupling
of two
one-dimensional
cells
can
produce
oscillation
even
though
neither
one
by itself
can
oscillate.
A central
question
about
coupled
cell
system
dynamics
concerns
the
relative
balance
between
the
internal
dynamics
of each
cell
and
the
way
the
cells
are
coupled.
Coupled
cell
systems
also
have
symmetry
(permutations
of the
cells
that
preserve
the
coupling),
which
often
organizes
much
of the
interesting
dynamics.
The
patterns
of oscillation
that
cell
systems
can
exhibit
depend
solely
on the
architecture
of the
cell
system,
as our
work
on animal
gaits
has
shown.
Coupled
cell
systems
can
be explored
by simulation
and
theory,
and
students
have
written
undergraduate,
masters,
and
PhD
theses
on the
subject.
For
example,
undergraduates
can
simulate
systems,
such
as a
four-cell
model
for
biped
locomotion
(that
models
differences
between
between
walk
and
run),
whereas
advanced
students
can
work
on the
sophisticated
dynamics,
symmetry-breaking
bifurcations,
and
pattern
formation
(as
in the
visual
cortex)
that
appear
in these
models.
The
mathematical
classification
of neuronal
bursting
states
has
been
an important
focus
of study
for
the
past
20 years.
Using
a combination
of theory
and
numerical
simulation,
patterns
of bursting
in coupled
cell
systems
will
be explored.
Einstein
Metrics
Project
(Bao)
Einstein
metrics
(the
Ricci
tensor
is a
multiple
of the
metric
tensor)
comprise
a major
focus
in differential
geometry.
These
metrics
are
more
general
than
those
with
constant
curvature
(the
space
forms);
nevertheless,
explicit
examples
are
scarce
and
graphical
descriptions
of known
examples
almost
totally
lacking.
Einstein
metrics
generalize
to Finsler
manifolds
(that
are
equipped
with
norms
instead
of inner
products).
Broadening
the
context
to Finsler
geometry
holds
promise
because
explicit
examples
of Einstein
metrics
are
available
among
a special
class
known
as Randers
spaces:
Riemannian
spaces
for
which
there
is a
preferred
direction
at each
point.
This
preferred
vector
field
can
arise
as the
distribution
of wind/fluid
velocities,
or magnetic
polarizations.
There
is an
ongoing
effort
to express
the
Einstein
condition
for
Randers
spaces
as a
system
of nonlinear
PDEs
coupling
the
Riemannian
metric
to the
preferred
vector
field.
This
project
can
initiate
undergraduates,
train
graduate
students,
and
supply
postdocs
with
interesting
problems.
Undergraduates
can
use
computer
software
to picture
the
geodesics
of known
examples
(Bass).
Graduate
students
can
work
on the
classification
of Randers
spaces
which
are
Einstein
(Robles).
Postdocs
can
focus
on the
construction
of Randers-Einstein
metrics
on spaces
with
interesting
topology.
This
project
has
an interdisciplinary
flavor.
Regard
the
preferred
vector
field
as the
steady-state
flow
of particles
in a
given
medium.
Model
the
Riemannian
metric
as the
warping
of space
(occupied
by the
medium)
due
to the
presence
of elastic
obstacles.
Alterations
in the
flow
reshape
the
elastic
obstacle,
and
vice
versa.
This
model
provides
a paradigm
for
understanding
the
coupling
between
the
Riemannian
metric
and
the
preferred
vector
field
(which
may
be visualized
using
large
scale
computing).
|