In summary: We have a convex wheel with a smooth boundary parameterized by

(over some range of r values) with the parameterization giving a counter-clockwise orientation. We compute the parameterization for the centroidal curve given by

Then we use conservation of energy to determine an ordinary differential equation for r(t), and we use information about the initial motion to determine a numerical solution (there is absolutely no hope of finding the exact solution). At time t, the rolling wheel has the parameterization

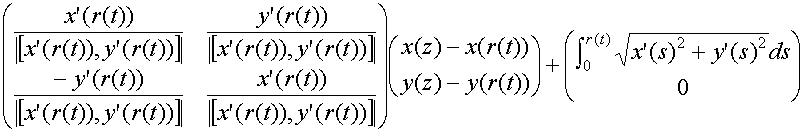
in terms of the parameterizing variable z. next