• HOME
• TEACHING
• RESEARCH
• CV
• PUBLICATIONS

Tsorng-Whay Pan's Selected Publications:

• Book:

  • R. Glowinski and T.-W. Pan, Numerical Simulation of Incompressible Viscous Flow: Methods and Applications, De Gruyter, Berlin/Boston, 2022:
    

    This book on finite element-based computational methods for solving incompressible viscous fluid flow problems shows readers how to apply operator splitting techniques to decouple complicated computational fluid dynamics problems into a sequence of relatively simpler sub-problems at each time step, such as hemispherical cavity flow, cavity flow of an Oldroyd-B viscoelastic flow, and particle interaction in an Oldroyd-B type viscoelastic fluid. Efficient and robust numerical methods for solving those resulting simpler sub-problems are introduced and discussed. Interesting computational results are presented to show the capability of methodologies addressed in the book.
    This book discusses finite element based computational methods for solving incompressible viscous fluid flow problems. Fundamental aspects of the computational methodologies, and extensions for advanced engineering applications are also presented.

• Selected Articles:

  1. Shang-Huan Chiu and T.-W. Pan
     A 3D DLM/FD method for simulating the motion of an ellipsoid in a bounded shear flow of viscoelastic fluids
     Annals of Mathematical Sciences and Applications Vol. 9, No. 1 (2024), pp. 91-121.
     

  2. T.-W. Pan and Shang-Huan Chiu
     A DLM/FD method for simulating balls settling in Oldroyd-B viscoelastic fluids
     Journal of Computational Physics 484 (2023), 112071
     

     In this article we present a numerical method for simulating the sedimentation of balls in a three-dimensional channel filled with an Oldroyd-B fluid. We have combined a distributed Lagrange multiplier/fictitious domain method with a factorization approach from Lozinski and Owens [J. Non-Newtonian Fluid Mech. 112 (2003) 161] via an operator splitting technique. The method is validated by comparing obtained results with those reported in literature. Then the study of fluid elasticity on the formation of ball chain (up to six balls) in Oldroyd-B fluids are presented to demonstrate the capability of our methods. For a higher value of elastic number, a longer chain of balls can be formed while settling in an Oldroyd-B fluid as observed experimentally. (A stable six-ball chain settling in an Oldroyd-B fluid is shown at the right.)
     

  3. T.-W. Pan, Shang-Huan Chiu, Aixia Guo, and Jiwen He
     Numerical study of transitions in lid-driven flows in shallow cavities
     Comptes Rendus. Mécanique 351 (S1) (2023), pp. 1-17.
     

  4. Ang Li, T.-W. Pan, and R. Glowinski
     On the DLM/FD methods for simulating neutrally buoyant swimmers moving in non-Newtonian shear thinning fluids
     International Journal for Numerical Methods in Fluids 94 (2022), 1465-1483.
     

  5. T.-W. Pan, Ang Li and R. Glowinski
     Numerical study of equilibrium radial positions of neutrally buoyant balls in circular Poiseuille flows
     Physics of Fluids 33 (2021), 033301.
     

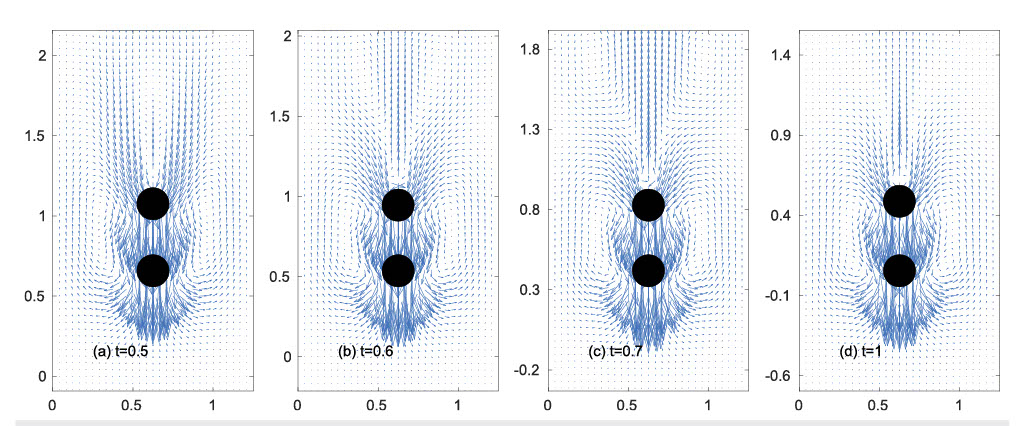  6. T.-W. Pan, Shang-Huan Chiu and R. Glowinski
     Numerical study of two balls settling in viscoelastic fluids from an initial vertical configuration
     Physics of Fluids 31 (2019), 123104 (Featured Article).
     

     In this article, we have investigated, via numerical simulation, the interaction of two identical balls settling in a vertical square tube filled with a viscoelastic fluid. For two balls released in Oldroyd-B fluids, one on top of the other initially, we have observed two possible scenarios, among others: either the trailing ball catches up the leading one to form a doublet (dipole) or the balls separate with a stable final distance. If the ball density is slightly larger than the fluid density, the two balls form a doublet, 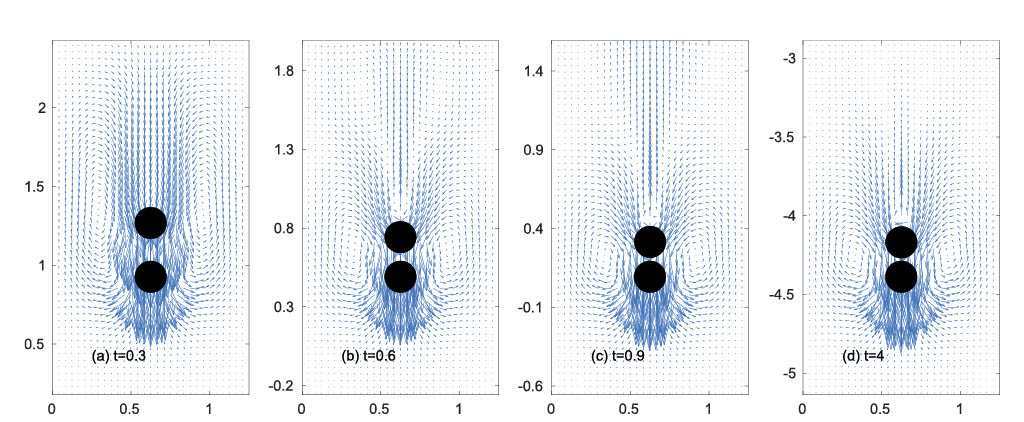either vertical or tilted. If one further increases the ball density, the two balls still form a doublet if the initial distance is small enough, but for larger initial distances at higher elasticity numbers, the balls move away from each other and their distance reaches a stable constant. Factors influencing doublet formation are (possibly among others) the ball density, the ball initial distance, and the fluid elasticity number. When settling in FENE-CR (finite extendable non-linear elastic - Chilcott and. Rallison) fluids, low values of the coil maximal extension limit enhance ball separation. (The effect of the initial distance on forming a doublet in an Oldroyd-B fluid is shown at the right two figures. The right top one shows that two balls keep a constant distance.)
     

  7. R. Glowinski and T.-W. Pan
     Two decades of wave-like equation for numerical simulating of incompressible viscous flow: a review
     In "Contributions to Partial Differential Equations and Applications" (Chetverushkin et al. eds.),
     Computational Methods in Applied Sciences, vol 47, pp. 221-250, Springer, Cham, 2019.
     

  8. T.-W. Pan and R. Glowinski
     Numerical study of spheres settling in Oldroyd-B fluids
     Physics of Fluids 30 (2018), 113102 (Editor's Pick Article).
     

  9. Liang-Hsia Tsai, Chien-Cheng Chang, T.-W. Pan, and R. Glowinski
     Numerical study of the wall effect on particle sedimentation
     International Journal of Computational Fluid Dynamics 32 (2018), 158-166.
     

  10. Shang-Huan Chiu, T.-W. Pan, and R. Glowinski
      A 3D DLM/FD method for simulating the motion of spheres in a bounded shear flow of Oldroyd-B fluids
      Computers & Fluids 172 (2018), 661-673; arXiv:1707.01957.
      

  11. Shihai Zhao, Yao Yu, T.-W. Pan, and R. Glowinski
      A DLM/FD/IB method for simulating compound cell Interacting with red blood cells in a microchannel
      Chinese Annals of Mathematics, Series B 39 (2018), 535-552.
      

  12. T.-W. Pan, Aixia Guo, Shang-Huan Chiu, and R. Glowinski
      A 3D DLM/FD method for simulating the motion of spheres and ellipsoids under creeping flow conditions
      Journal of Computational Physics 352 (2018), 410-425.
      

  13. T.-W. Pan and R. Glowinski
      Numerical study of two disks settling in an Oldroyd-B fluid: From periodic interaction to chaining
      Physical Review E 96 (2017), 063103; arXiv:1607.06009.
      

  14. Aixia Guo, T.-W. Pan, Jiwen He, and R. Glowinski
      Numerical methods for simulating the motion of porous balls in simple 3D shear flows under creeping conditions
      Computational Methods in Applied Mathematics 17 (2017), 397-412.
      

  15. T.-W. Pan and R. Glowinski
      Dynamics of particle sedimentation in viscoelastic fluids: A numerical study on particle chain in two-dimensional narrow channel
      Journal of Non-Newtonian Fluid Mechanics 244 (2017), 44-56.
      

  16. Lingling Shi, Suncica Canic, Annalisa Quaini, and T.-W. Pan
      A study of self-propelled elastic cylindrical micro-swimmers using modeling and computation
      Journal of Computational Physics 314 (2016), 264–286.
      

  17. Xiting Niu, Lingling Shi, T.-W. Pan, and R. Glowinski
      Numerical simulation of the motion of inextensible capsules in shear flow under the effect of the nature state
      Communications in Computational Physics 18 (2015), 787-807.
      

  18. Shih-Lin Huang, Shih-Di Chen, T.-W. Pan, Chien-Cheng Chang, and Chin-Chou Chu
      The motion of a neutrally buoyant particle of an elliptic shape in two dimensional shear flow: a numerical study
      Physics of Fluids 27 (2015), 083303.
      

  19. T.-W. Pan, Shihai Zhao, Xiting Niu, and R. Glowinski
      A DLM/FD/IB method for simulating compound vesicle motion under creeping flow condition
      Journal of Computational Physics 300 (2015), 241-253.
      

  20. Xiting Niu, T.-W. Pan, and R. Glowinski
      The dynamics of inextensible capsules in shear flow under the effect of the natural state
      Biomechanics and Modeling in Mechanobiology 14 (2015), 865-876.
      

  21. Alexandre Caboussat, R. Glowinski, T.-W. Pan
      On the numerical solution of some eikonal equations: an elliptic solver approach
      Chin. Ann. Math. 36B (2015), 689–702.
      

  22. Che-Ming Shih, Chun-Fei Kung, Chien-Cheng Chang and T.-W. Pan
      Self-organized capacity for energy extraction by clustering particles in two-species suspension flow at small Reynolds numbers
      Applied Physics Letters 106 (2015), 024102.
      

  23. Shihai Zhao, T.-W. Pan
      Numerical simulation of red blood cell suspensions behind a moving interface in a capillary
      Numerical Mathematics: Theory, Methods and Applications 7 (2014), 499-511.
      

  24. Lingling Shi, T.-W. Pan, R. Glowinski
      Three-dimensional numerical simulation of red blood cell motion in Poiseuille flows
      Int. J. Numer. Methods Fluids 76 (2014), 397-415.
      

  25. Lingling Shi, Yao Yu, T.-W. Pan, R. Glowinski
      Oscillating motions of neutrally buoyant particle and red blood cell in Poiseuille flow in a narrow channel
      Physics of Fluids 26 (2014), 041904.
      

  26. Suchung Hou, T.-W. Pan, R. Glowinski
      Circular band formation for incompressible viscous fluid-rigid particle mixtures in a rotating cylinder
      Physical Review E 89 (2014), 023013.
      

  27. T.-W. Pan, Shih-Lin Huang, Shih-Di Chen, Chin-Chou Chu, Chien-Cheng Chang
      A numerical study of the motion of a neutrally buoyant cylinder in two dimensional shear flow
      Computers & Fluids 87 (2013), 57-66.
      

  28. Lingling Shi, T.-W. Pan, R. Glowinski
      Lateral migration and equilibrium shape and position of a single red blood cell in bounded Poiseuille flows
      Physical Review E 86 (2012), 056308.
      

  29. Shih-Di Chen, T-W Pan, Chien-Cheng Chang
      The motion of a single and multiple neutrally buoyant elliptical cylinders in plane Poiseuille flow
      Physics of Fluids 24 (2012), 103302.
      

  30. Lingling Shi, T.-W. Pan, R. Glowinski
      Deformation of a single blood cell in bounded Poiseuille flows
      Physical Review E 85 (2012), 016307.
      

  31. Lingling Shi, T.-W. Pan, R. Glowinski
      Numerical simulation of lateral migration of red blood cells in Poiseuille flows
      Int. J. Numer. Methods Fluids 68 (2012), 1393-1408.
      

  32. T.-W. Pan, Lingling Shi, R. Glowinski
      A DLM/FD/IB method for simulating cell/cell and cell/particle interaction in microchannels
      Chinese Annals of Mathematics, Series B 31 (2010) 975-990.
      

  33. H. Antil, R. Glowinski, R. H.W. Hoppe, C. Linsenmann, T.-W. Pan, A. Wixforth
      Modeling, simulation, and optimization of surface acoustic wave driven microfluidic biochips
      Journal of Computational Mathematics 28 (2010) 149-169.
      

  34. Tong Wang, T.-W. Pan, R. Glowinski
      A fictitious domain method for simulating viscous flow in a constricted elastic tube subject to a uniform external pressure
      International Journal for Numerical Methods in Biomedical Engineering 26 (2010) 290-304.
      

  35. Tong Wang, T.- W. Pan, Z. Xing, R. Glowinski
      Numerical simulation of rheology of red blood cell rouleaux in microchannels
      Physical Review E 79 (2009), 041916
      

  36. T.-W. Pan, Tong Wang
      Dynamical simulation of red blood cell rheology in microvessels
      International Journal of Numerical Analysis and Modeling 6 (2009), 455-473.
      

  37. Jian Hao, T.-W. Pan, S. Canic, R. Glowinski, D. Rosenstrauch
      A fluid-cell interaction and adhesion algorithm for tissue-coating of cardiovascular implants
      SIAM Journal on Multiscale Modeling and Simulation 7 (2009), 1669-1694.
      

  38. Jian Hao, T.-W. Pan, R. Glowinski, D.D. Joseph
      A fictitious domain/distributed Lagrange multiplier method for the particulate flow of Oldroyd-B fluids: A positive definiteness preserving approach
      Journal of Non-Newtonian Fluid Mechanics 156 (2009), 95-111.
      

  39. T.-W. Pan, Jian Hao, R. Glowinski
      On the simulation of a time-dependent cavity flow of an Oldroyd-B fluid
      International Journal for Numerical Methods in Fluids 60 (2009) 791-808.
      

  40. T.-W. Pan, C.-C. Chang, R. Glowinski
      On the motion of a neutrally buoyant ellipsoid in a three-dimensional Poiseuille flow
      Computer Methods in Applied Mechanics and Engineering 197 (2008), 2198-2209.
      

  41. R. Glowinski, E. Dean, G. Guidoboni, L.H. Juarez V., T.-W. Pan
      Operator-splitting methods for the numerical simulation of particulate and free-surface flows and for the numerical solution of elliptic Monge-Ampere equation
      Japan Journal of Industrial and Applied Mathematics 25 (2008), 1-63.
      

  42. Tong Wang, T.-W. Pan, R. Glowinski
      A comparison of L2-projection and H1-projection methods for the numerical simulation of incompressible viscous fluid flow: A case study
      Chinese Journal of Engineering Mathematics 25 (2008), 761-778.
      

  43. T.-W. Pan, R. Glowinski, Suchung Hou
      Direct numerical simulation of pattern formation in a rotating suspension of non-Brownian settling particles in a fully filled cylinder
      Computers & Structures 85 (2007), 955-969.
      

  44. T.-W. Pan, Jian Hao
      Numerical Simulation of a lid-driven cavity viscoelastic flow at high Weissenberg numbers
      Comptes Rendus Mathematique , 344 (2007), 283-286.
      

  45. Jian Hao, T.-W. Pan
      Simulation for high Weissenberg number: Viscoelastic flow by a finite element method
      Applied Mathematics Letters 20 (2007), 988-993.
      

  46. R. Glowinski, T.-W. Pan, L.H. Juarez, E. Dean
      Finite element methods for the numerical simulation of incompressible viscous fluid flow modeled by the Navier-Stokes equations. III.
      Bol. Soc. Esp. Mat. Apl. SeMA 38 (2007), 11–37.
      

  47. R. Glowinski, T.-W. Pan, J. Periaux
      Numerical simulation of a multi-store separation phenomenon: A fictitious domain approach
      Computer Methods in Applied Mechanics and Engineering 195 (2006), 5566-5581.
      

  48. R. Glowinski, G. Guidoboni, T.-W. Pan
      Wall-driven incompressible viscous flow in a two-dimensional semi-circular cavity
      Journal of Computational Physics 216 (2006), 79-91.
      

  49. R. Glowinski, T.-W. Pan, L.H. Juarez, E. Dean
      Finite element methods for the numerical simulation of incompressible viscous fluid flow modeled by the Navier-Stokes equations. II.
      Bol. Soc. Esp. Mat. Apl. SeMA 37 (2006), 11–46.
      

  50. R. Glowinski, T.-W. Pan, L.H. Juarez, E. Dean
      Finite element methods for the numerical simulation of incompressible viscous fluid flow modeled by the Navier-Stokes equations. I.
      Bol. Soc. Esp. Mat. Apl. SeMA 36 (2006), 7–62.
      

  51. T.-W. Pan, R. Glowinski, D.D. Joseph
      Simulating the dynamics of fluid-cylinder interactions
      Journal of Zhejiang University Science 6A (2005), 97-109.
      

  52. T.-W. Pan, R. Glowinski, D.D. Joseph
      Simulating the dynamics of fluid-ellipsoid interactions
      Computers and Structures 83 (2005), 463-478.
      

  53. B.H. Yang, J. Wang, D.D. Joseph, H.H. Hu, T.-W. Pan, R. Glowinski
      Migration of a sphere in tube flow
      Journal of Fluid Mechanics 540 (2005), 109-131.
      

  54. T.-W. Pan, R. Glowinski
      Direct simulation of the motion of neutrally buoyant balls in a three-dimensional Poiseuille flow
      C. R. Mecanique, Acad. Sci. Paris 333 (2005), 884-895.
      

  55. L.H. Juarez, R. Glowinski, T.-W. Pan
      Numerical simulation of fluid flow with moving and free boundaries
      Boletin de la Sociedad Espanola de Matematica Aplicada 30 (2004), 49-102.
      

  56. N. R. Amundson, T.-W. Pan, V. I. Paulsen
      Diffusion with Stefan and Maxwell
      AIChE Journal 49 (2003), 813-830.
      

  57. R. Glowinski, Y.A. Kuznetsov, T.-W. Pan
      A penalty/Newton/conjugate gradient method for the solution for obstacle problems
      Comptes Rendus Mathematique, 336 (2003), 435-440.
      

  58. B. Dacorogna, R. Glowinski, T.-W. Pan
      Numerical methods for the solution of a system of Eikonal equations with Dirichlet boundary condition
      Comptes Rendus Mathematique, 336 (2003), 511-518.
      

  59. T.-W. Pan, D.D. Joseph, R. Bai, R. Glowinski, V. Sarin
      Fluidization of 1204 spheres: simulation and experiments
      Journal of Fluid Mechanics 451 (2002), 169-191.
      

  60. L.H. Juarez, R. Glowinski, T.-W. Pan
      Numerical simulation of the sedimentation of rigid bodies in an incompressible viscous fluid by Lagrange multiplier/fictitious domain methods combined with the Taylor-Hood finite element approximation
      Journal of Scientific Computing 17 (2002), 683-694.
      

  61. T.-W. Pan, R. Glowinski
      Direct simulation of the motion of neutrally buoyant circular cylinders in plane Poiseuille flow
      Journal of Computational Physics 181 (2002), 260-279.
      

  62. T.-W. Pan, R. Glowinski, G.P. Galdi
      Direct simulation of the motion of a settling ellipsoid in Newtonian fluid
      Journal of Computational and Applied Mathematics 149 (2002), 71-82.
      

  63. T.-W. Pan, D.D. Joseph, R. Glowinski
      Modeling Rayleigh-Taylor instability of a sedimenting suspension of several thousand circular particles in direct numerical simulation
      Journal of Fluid Mechanics 434 (2001), 23-37.
      

  64. R. Glowinski, T.-W. Pan, T. I. Hesla, D. D. Joseph, J. Periaux
      A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: Application to particulate flow
      Journal of Computational Physics 169 (2001), 363-427.
      

  65. T.-W. Pan
      Numerical simulation of the motion of neutrally buoyant particles in the plane Poiseuille flow of a Newtonian fluid
      C. R. Acad. Sci. Paris, Serie IIb, 329 (2001), 435-438.
      

  66. N. A. Patankar, P. Singh, D. D. Joseph, R. Glowinski, T.-W. Pan
      A new formulation of the distributed Lagrange multiplier/fictitious domain method for particulate flows
      Int. J. Multiphase Flow 26 (2000), 1509-1524.
      

  67. P. Singh, D. D. Joseph, T. I. Hesla, R. Glowinski, T.-W. Pan
      A distributed Lagrange multiplier/fictitious domain method for viscoelastic particulate flows
      J. Non-Newtonian Fluid Mech. 91 (2000), 165-188.
      

  68. R. Glowinski, T.-W. Pan, T. I. Hesla, D. D. Joseph, J. Periaux
      A distributed Lagrange multiplier/fictitious domain method for the simulation of flows around moving rigid bodies: Application to particulate flow
      Computer Methods in Applied Mechanics and Engineering 184 (2000), 241-267.
      

  69. T.-W. Pan, V. Sarin, R. Glowinski, J. Periaux, A. Sameh
      Parallel solution of multibody store separation by a fictitious domain method
      in Parallel CFD '99, D. Keyes ed., North-Holland, Amsterdam, 2000, 329-336.
      

  70. T.-W. Pan, R. Glowinski
      A projection/wave-like equation method for the numerical simulation
      of incompressible viscous fluid flow modeled by the Navier-Stokes equations
      Computational Fluid Dynamics Journal 9 (2000), 28-42.
      

  71. T.-W. Pan
      Existence and multiplicity of radial solutions describing the equilibrium of nematic liquid crystals on annular domains
      Journal of Mathematical Analysis and Applications 245 (2000), 266-281.
      

  72. R. Glowinski, T.-W. Pan, T. I. Hesla, D.D. Joseph
      A distributed Lagrange multiplier/fictitious domain method for particulate flows
      International Journal of Multiphase Flow 25 (1999), 755-794.
      

  73. R. Glowinski, T.-W. Pan, T. I. Hesla, D. D. Joseph, J. Periaux
      A distributed Lagrange multiplier/fictitious domain method for flows around moving rigid bodies: Application to particulate flow
      International Journal for Numerical Methods in Fluids 30 (1999), 1043-1066.
      

  74. T.-W. Pan
      Numerical simulation of the motion of a ball falling in an incompressible viscous fluid
      C. R. Acad. Sci. Paris , Serie IIb 327 (1999), 1035-1038.
      

  75. R. Glowinski, T.-W. Pan, J. Periaux
      Distributed Lagrange multiplier methods for incompressible viscous flow around moving rigid bodies
      Computer Methods in Applied Mechanics and Engineering 151 (1998), 181-194.
      

  76. T.-W. Pan
      Error estimates for a fictitious domain method with Lagrange multiplier treatment on the boundary for a Dirichlet problem
      Japan Journal of Industrial and Applied Mathematics 15 (1998), 75-85.
      

  77. R. Glowinski, T.-W. Pan, J. Periaux
      A Lagrange multiplier/fictitious domain method for the numerical simulation of incompressible viscous flow around moving rigid bodies (I): The case where the rigid body motions are known a priori
      C. R. Acad. Sci. Paris, Serie I 324 (1997), 361-369.
      

  78. T.-W. Pan
      On the existence of infinitely many limit points on the solution branch of planar shear flow of nematic liquid crystals
      Journal of Mathematical Analysis and Applications 208 (1997), 120-140.
      

  79. R. Glowinski, T.-W. Pan, R. O. Wells, X. Zhou
      Wavelet and finite element solutions for the Neumann problem using fictitious domains
      Journal of Computational Physics 126 (1996), 40-51.
      

  80. J. Feng, D. D. Joseph, R. Glowinski, T.-W. Pan
      A three-dimensional computation on the force and moment on an ellipsoid settling slowly through a viscoelastic fluid
      Journal of Fluid Mechanics 283 (1995), 1-16.
      

  81. R. Glowinski, T.-W. Pan, J. Periaux
      A Lagrange multiplier/fictitious domain method for the Dirichlet problem. Generalization to some flow problems
      Japan Journal of Industrial and Applied Mathematics 12 (1995), 87-108.
      

  82. R. Glowinski, A. J. Kearsley, T.-W. Pan, J. Periaux
      Numerical simulation and optimal shape for viscous flow by fictitious domain method
      International Journal for Numerical Methods in Fluids 20 (1995), 695-711.
      

  83. R. Glowinski, T.-W. Pan, J. Periaux
      A fictitious domain method for external incompressible viscous flow modeled by Navier-Stokes equations
      Computer Methods in Applied Mechanics and Engineering 112 (1994), 133-148.
      

  84. R. Glowinski, T.-W. Pan, J. Periaux
      A fictitious domain method for Dirichlet problem and applications
      Computer Methods in Applied Mechanics and Engineering 111 (1994), 283-303.
      

  85. G. Liao, T.-W. Pan, J. Su
      Numerical grid generator based on Moser's deformation method
      Numerical Methods for Partial Differential Equations 10 (1994), 21-31.
      

  86. R. Glowinski, T.-W. Pan
      Error estimates for fictitious domain/penalty/finite element methods
      CALCOLO 29 (1992), 125-141.
      

  87. M. Luskin, T.-W. Pan
      Nonplanar shear flows for nonaligning nematic liquid crystals
      Journal of Non-Newtonian Fluid Mechanics 42 (1992), 369-384.