 |
Undergraduate
Colloquium |
 |
 |
> Current AY
> Previous talks
> TX-LA conferences:
— UH,
Nov. 11-12, 2017
— LSU,
Oct. 5, 2018
— TAMU,
Oct. 19-20, 2019
— online,
Oct. 31-Nov. 1, 2020
— UH,
Mar. 26-27, 2022
— LSU,
Mar. 25-26, 2023
— TAMU,
Mar. 23-24, 2024
— UH,
Mar. 22-23, 2025
> Putnam Math Competition
>
Math Colloquium
|
 |
 |
 |
 |
|
 |
 |
 |
 |
Print
Announcement
Neil Jerome A. Egarguin
University of Houston
Defect Detection in a One-dimensional Spring-Mass System
February 7, 2019
5:00pm PGH 646
|
Abstract
|
|
|
|
Detecting defects in physical systems using external or easily
accessible measurements had been widely studied in the context of
optics, electromagnetism, nanotechnology, metamaterials and other
industrial and mechanical applications. Spring-mass systems are
commonly used as simple models for some of these physical systems. In
this talk, we shall discuss the development of a defect detection
scheme in a one-dimensional Hookean spring-mass system. We shall
consider a coupled spring-mass system in which the nodes are of unit
mass, except for some defective nodes. The goal is to determine the
location and/or the mass of the defects using some measurements
obtained from the first mass. These measurements involve the
longitudinal vibrations due to a unit impulse applied to the first
mass.
The scheme we developed relies on the Laplace transform of the system
of ODEs modelling the vibrations in the spring-mass system and some
optimization techniques. The talk will highlight the derivation of the
defect detection strategy, as well as some numerical results. Towards
the end of the talk, we shall also look at some possible extensions of
this work such as designing algorithms for systems with varying
stiffness coefficient and the use of better numerical minimization
procedures, and other related research topics for undergraduate
students.
This talk is based on a research project with Noam Harari (UH
undergraduate student) and Dr. Daniel Onofrei.
Pizza will be served.

A spring-mass system with defect at location j
|
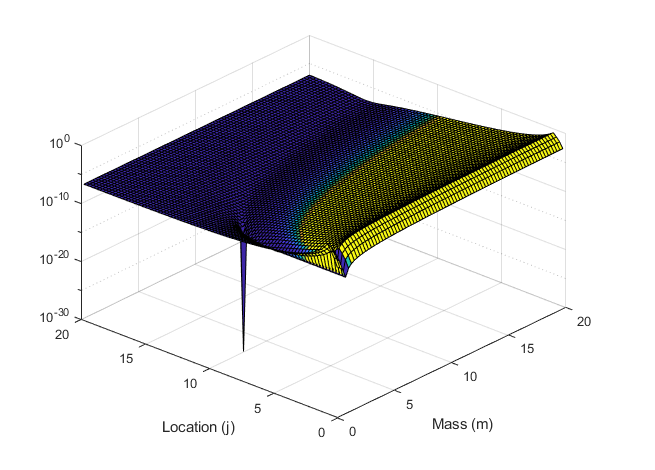
Plot of the residual function showing the location and mass of the
defect
|
|
|
 |
 |
 |
 |
|
|

