RESEARCH
Nonlocal Diffusion and Pattern Formation in Biological Systems
Many biological and physical systems are known for exhibiting interesting periodic structures, like striped and spot patterns. In many instances, like in the case of chemical reactions, these structures emerge from the interaction of two competing processes that lead to an instability. Roughly, the first mechanism relates to the intrinsic behavior of the system, while the second one corresponds to a transport, or diffusion process. While in most cases diffusion is the correct mechanism to consider, in many biological applications it does not capture the observed behavior. This is particularly true when modeling dispersion of populations or plant seeds, or when looking at hunting or foraging behavior of certain animals. In this project we investigate how these nonlocal forms of dispersal affect pattern formation in physical and biological applications.Nonlocal Effects in Oscillatory Media
Oscillatory media is known for creating beautiful patterns like spiral, target, and traveling waves. At the heart of these systems there are two mechanisms whose interaction contributes to the formation of these structures. One is the intrinsic dynamics of the system, which leads to oscillations and justifies the name oscillatory media. The second mechanism is the interaction, or coupling, that takes place between these `oscillators'. In many cases this coupling is well approximated by a local diffusion process. However, when nonlocal interactions become important, they can lead to novel structures called spiral chimeras (figures a) and b) ). As a first step in understanding the formation of these new patterns, this project focuses on rigorously deriving amplitude equations for these systems and showing existence of target patterns and spiral waves.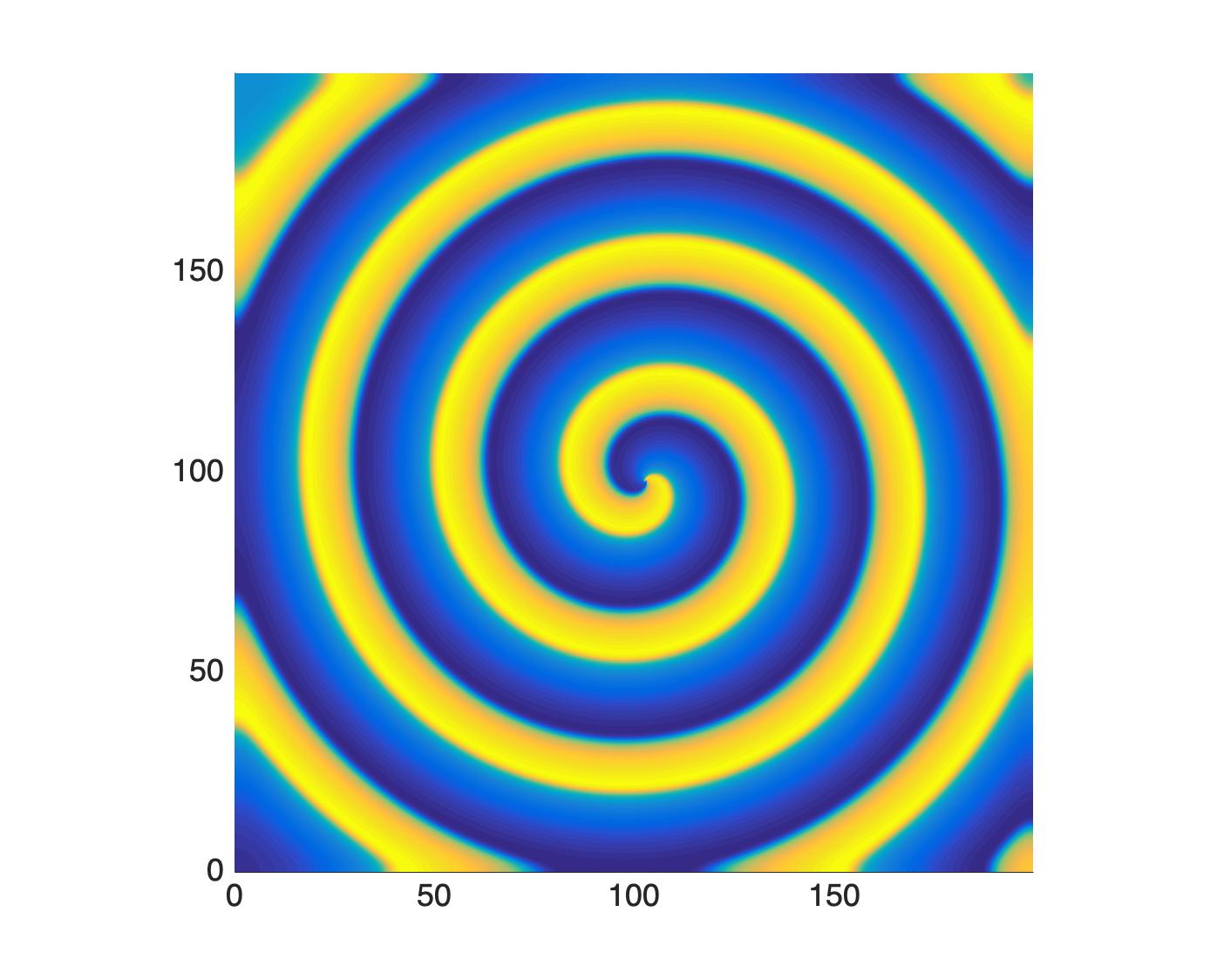
a)
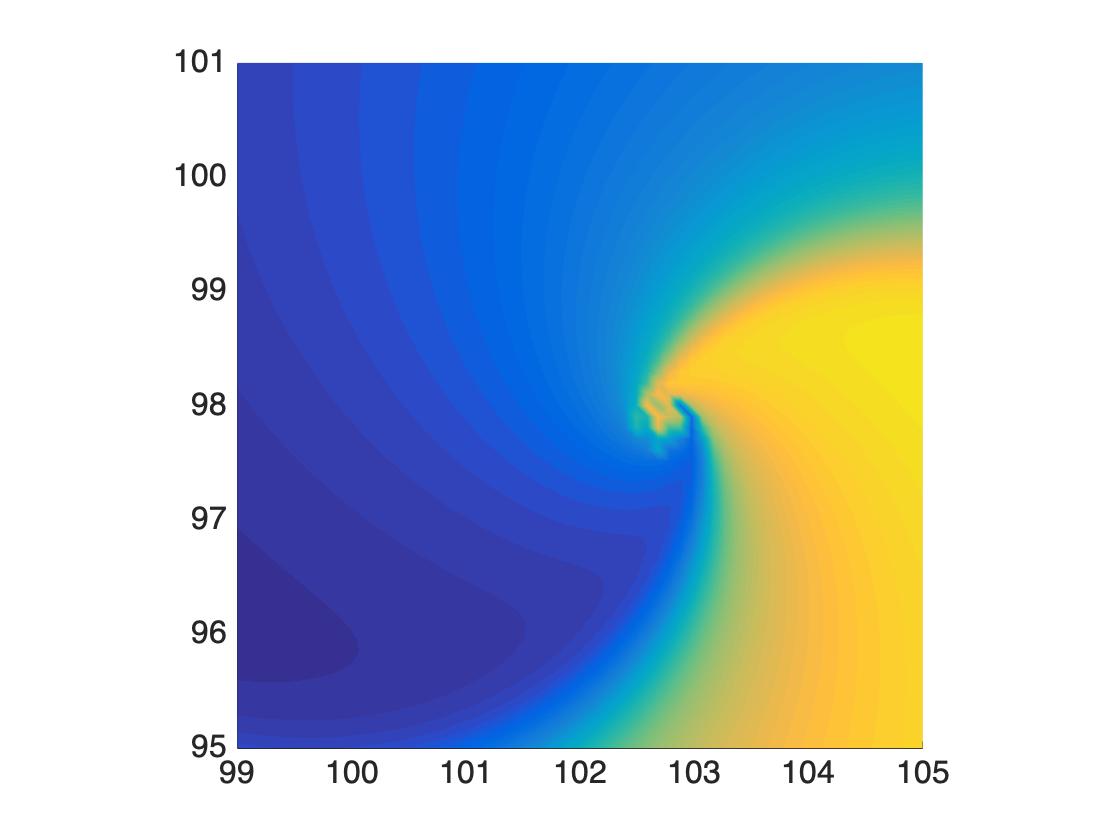
b)
Defects
Defects and impurities in pattern-forming systems can modify existing patterns or create new structures. For example, defects in convection phenomena lead to deformed striped patterns (figure a) ), whereas in oscillatory media they create target patterns (figures b) and c) ). In these examples, impurities are localized areas where the properties of the medium are different. As a result these inhomogeneities can be modeled as perturbations of the amplitude equations that describe these systems. One then hopes to prove existence of these altered patterns using perturbation theory. The main difficulty with this approach is that the linearization about the steady states is in general not an invertible operator in regular Sobolev spaces. Thus, my research focuses on developing methods to make these linear operators Fredholm so that regular perturbation techniques can be employed to find these solutions.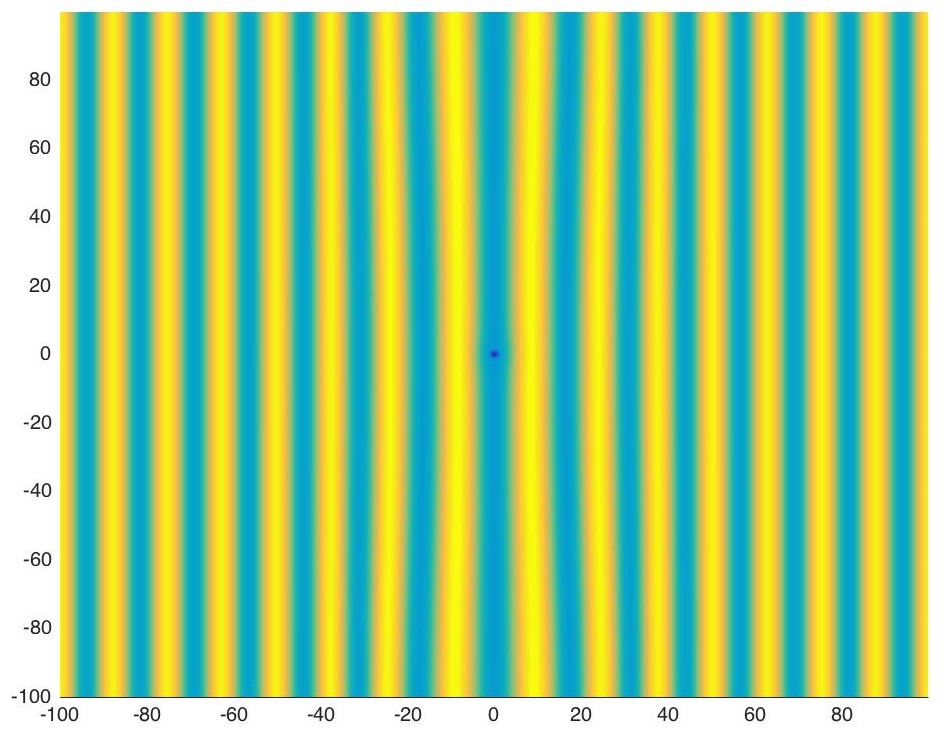
a)
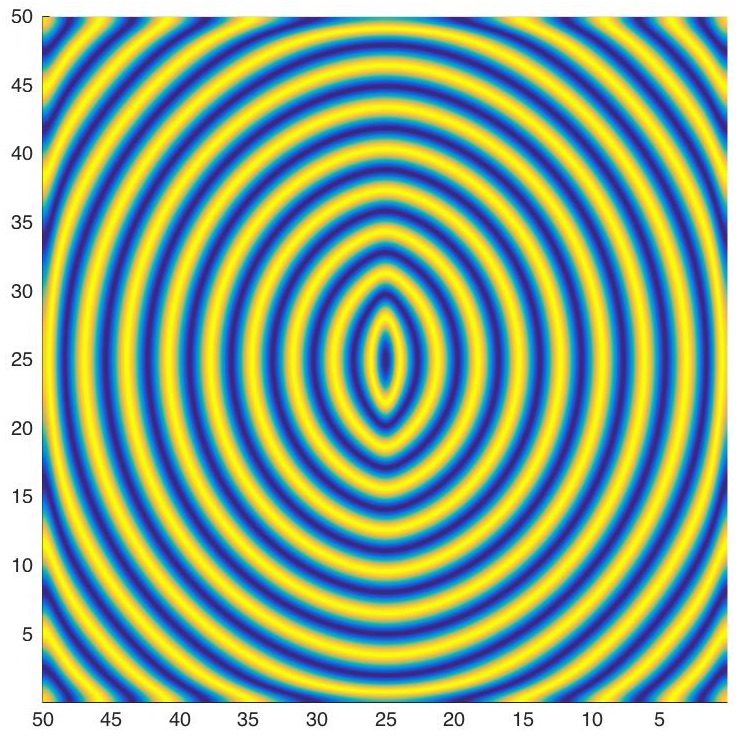
b)
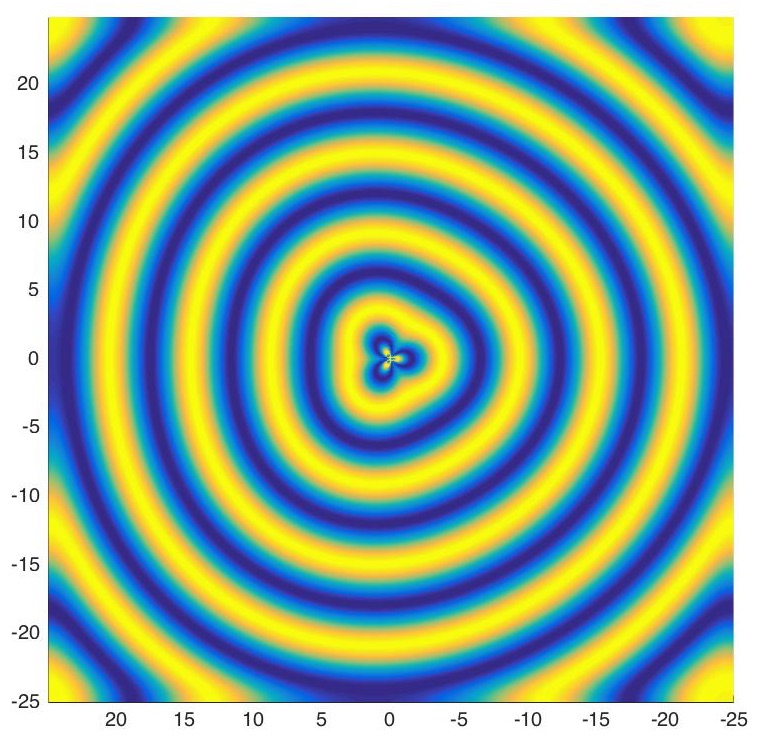
c)
PUBLICATIONS
- L. Cappanera, G. Jaramillo. The role of boundary constraints in simulating biological systems with nonlocal dispersal. In preparation
- G. Jaramillo, C. Meraz. Existence of weak solutions for a nonlocal Klausmeier model. In preparation
- G. Jaramillo. Existence of spiral waves in nonlocal oscillatory media. Submitted (2024)
- L. Cappanera, G. Jaramillo, C. Ward. Analysis and simulation of a nonlocal Gray-Scott model. Accepted SIAM Journal on Applied Mathematics (2024).
- G. Jaramillo, L. Mrad, TL Stepien. Dynamics of a linearly-perturbed May-Leonard competition model. Chaos(2023). See also DOI
- G. Jaramillo. Can large inhomogeneities generate target patterns? ZAMP (2023). See also DOI
- G. Jaramillo. Rotating spirals in oscilatory media with nonlocal interactions and their normal form. Discrete Contin. Dyn. Syst. - S (2022). See also DOI
- L. Cappanera, G. Jaramillo, C. Ward. Numerical Methods for a Diffusive Class of Nonlocal Operators. J. Sci. Comput. (2021). See also DOI
- G. Jaramillo, S. Venkataramani. A Modified Split-Bregman Algorithm for Computing Microstructures Through Young Measures. SIAM MMS (2019). See also DOI
- G. Jaramillo, S. Venkataramani. Target Waves in Nonlocal 2-d Arrays of Oscillators. Nonlinearity (2018). See also DOI
- G. Jaramillo, A. Scheel, Q. Wu. The Effect of Impurities on Striped Phases. Proc. Roy. Soc. Edinb.(2018). See also DOI
- G. Jaramillo, A.
Scheel. Pacemakers in a Large Array of Nonlocal
Oscillator. J. Differ. Equation. (2016). See also DOI
- G. Jaramillo. Inhomogeneities in 3 Dimensional Oscillatory Media. Networks and Heterogeneous Media (2015). See also DOI
- G. Jaramillo, A. Scheel. Deformation of Striped Patterns by Inhomogeneities. Math. Method. App. Sci.(2013). See also DOI