
A sketch of abdominal aneurysm (left) and a sketch of a stent
inserted in the abdominal aorta (right), not showing the aneurysm sac
1. Biomedical background and objectives
The research in this proposal
has been motivated by a study of blood flow through compliant vessels
after endovascular repair. The PI and cardiologist Dr. Krajcer at
St. Luke's Episcopal Hospital in Houston have begun a study of
blood flow through the abdominal aorta after the insertion of a
prosthesis (a spring-like device called stent)
used to treat abdominal aneurysm (sac-like protrusion
of weakened sections of the aorta).
See Figure 1.
The procedure entails inserting a stent inside the aneurysm where it
serves to hold open the weakened artery and to exclude
the aneurysm from circulation.
The main goal of this collaborative study is to understand the behavior
of the prosthesis and of the walls of the aorta subject to the
pressures induced by pulsatile blood flow.

The model
equations are obtained using asymptotic reduction of the
axi-symmetric Navier-Stokes equations in narrow and long channels. The
equations have first been derived in [2],
and a mathematically rigorous asymptotic reduction is presented in [5].
The equations are in the form of a quasilinear hyperbolic system of
partial differential equations
describing conservation of mass and momentum
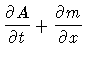 |
= | 0, | (1) |
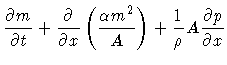 |
= | f(A,m). | (2) |
 accounts
for the fact that averaged quantities (momentum)
are conserved.
The source term
accounts
for the fact that averaged quantities (momentum)
are conserved.
The source term  includes the
effects of viscosity
includes the
effects of viscosity 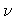 via
via
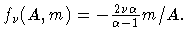 To close the system, the
pressure term needs to be specified [6]
To close the system, the
pressure term needs to be specified [6]
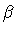 describes linear/nonlinear
behavior of the channel wall (pressure-strain relationship).
Versions of this model
have been used by many authors
to model fluid flow in compliant tubes
[1, 2, 4, 5, 6, 7, 8, 11, 15, 18].
A novel approach in this study is to assume that the coefficient G0
is a piecewise constant function of x to reflect the fact that
the stent and the aorta
have different elastic properties [20, 14].
As a consequence, stent and the aorta respond differently
to the pressure induced by the pulsatile blood flow
(see movies).
Various complications associated with this phenomenon
have been reported in patient studies [19].
The main objective of the present study is to analyze the abrupt
changes in the cross-sectional area due to the abrupt changes in the
elasticity coefficient G0,
understand their consequences on the blood flow,
and study optimal design of multiple overlapping stents
in order to minimize harmful effects caused by the perturbed channel
wall dynamics.
describes linear/nonlinear
behavior of the channel wall (pressure-strain relationship).
Versions of this model
have been used by many authors
to model fluid flow in compliant tubes
[1, 2, 4, 5, 6, 7, 8, 11, 15, 18].
A novel approach in this study is to assume that the coefficient G0
is a piecewise constant function of x to reflect the fact that
the stent and the aorta
have different elastic properties [20, 14].
As a consequence, stent and the aorta respond differently
to the pressure induced by the pulsatile blood flow
(see movies).
Various complications associated with this phenomenon
have been reported in patient studies [19].
The main objective of the present study is to analyze the abrupt
changes in the cross-sectional area due to the abrupt changes in the
elasticity coefficient G0,
understand their consequences on the blood flow,
and study optimal design of multiple overlapping stents
in order to minimize harmful effects caused by the perturbed channel
wall dynamics.
2. Mathematical
background and
objectives
In order to study discontinuities in the cross-sectional area we need
to be able to define a weak solution for a quasilinear system of
hyperbolic equations with discontinuous coefficients.
There is no general theory that deals with systems of hyperbolic
partial differential equations with discontinuous coefficients. The
literature is sparse even for hyperbolic equations in conservation form
allowing discontinuous coefficients.
There are various difficulties associated with the solutions
of such systems.
For example, physically reasonable solutions exhibit jump
discontinuities that are not compressive
because the jump discontinuity in the solution is induced by the
discontinuity in the coefficients,
and not by the compressive nature of the characteristics.
Deriving the ``correct'' entropy criterion for such jump
discontinuities,
and capturing such solutions numerically, is a problem.
In the case when the equations are not in conservation form, as in the
case of our model,
even the basic issue such as the meaning of the weak form of the
equations
in unclear. The main difficulty stems from the fact that the weak form
of the equations contains the products of the
Dirac measure by the Heaviside function which cannot be
defined in the sense of distributions.
In the case when the equations are linear and in conservation form there is a theory developed in [9] that deals with numerical approximation of one-dimensional linear conservation equations with discontinuous coefficients. Unfortunately, the techniques used in [9] do not generalize to nonlinear problems. Quasilinear scalar hyperbolic problems have been studied in [16, 17] where variational methods were used to study existence and uniqueness of solutions. The methods heavily rely on the fact that there is only one hyperbolic equation under consideration and it is unlikely that the approach can be generalized to systems. Finally, the most relevant to this proposal are the work of A.I Volpert [21] and a work by Dal Maso, P.G. LeFloch and F. Murat [12] where issues related to the product of the Dirac measure by the Heaviside function are discussed. Although these works do not deal with hyperbolic problems with discontinuous coefficients, the ideas about the meaning of the ambiguous products are very much related to the problems that arise in hyperbolic equations with discontinuous coefficients. In the work proposed here one of the objectives is to generalize those ideas to the systems with discontinuous coefficients.
1. Theoretical approach
To study weak solutions of equations (1)
and (2)
we begin with the standard approach:
multiply the equations by a test function
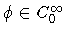 and
integrate by parts to obtain
and
integrate by parts to obtain
To get around
this difficulty we take the following approach.
Motivated by the underlying application in which the Young's modulus
coefficient
G0 is actually continuous, with high gradients at the
anchoring cites of the stent, we regularize the problem by smoothing
out the Dirac measure term G0'.
We regularize Dirac measure by using, the so called, admissible
averaging kernels [21]
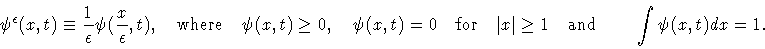
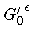 ,
and define the weak form of the original, singular problem
to be the one obtained in the limit, as
,
and define the weak form of the original, singular problem
to be the one obtained in the limit, as 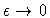 ,
of the regularized forms. In order for the limit to be defined, we need
to specify the term
,
of the regularized forms. In order for the limit to be defined, we need
to specify the term
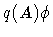 with respect to the measure G0'
approximated by the
admissible averaging kernels
with respect to the measure G0'
approximated by the
admissible averaging kernels 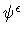 ,
[4, 21].
It can be shown that if the kernel is symmetric,
i.e., if
,
[4, 21].
It can be shown that if the kernel is symmetric,
i.e., if 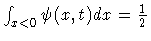 ,
then the resulting symmetric mean does not depend on the choice
of the symmetric kernel [4,
21].
The choice of the kernel
will depend on the particular problem at hand,
and here is where the ``physics'' of the problem needs to be taken into
account in order to recover the ``physically''
or ``physiologically reasonable solution''.
Although this is similar to the viscosity solutions approach in
the theory of conservation laws,
the underlying issues of convergence and stability require different
techniques. One of the goals of this project is to generalize the
techniques presented in [12]
to study convergence and stability of the products like (6)
arising in systems with discontinuous coefficients.
,
then the resulting symmetric mean does not depend on the choice
of the symmetric kernel [4,
21].
The choice of the kernel
will depend on the particular problem at hand,
and here is where the ``physics'' of the problem needs to be taken into
account in order to recover the ``physically''
or ``physiologically reasonable solution''.
Although this is similar to the viscosity solutions approach in
the theory of conservation laws,
the underlying issues of convergence and stability require different
techniques. One of the goals of this project is to generalize the
techniques presented in [12]
to study convergence and stability of the products like (6)
arising in systems with discontinuous coefficients.
 ,
and below the smoothing effects of the discontinuous coefficient G0.
Similar analysis needs to be performed before using the second-order
LW-method. The issues here are related to balancing the effects of
numerical dispersion, numerical diffusion and large artificial source
terms,
with the regularization of G0 and with the source
term
,
and below the smoothing effects of the discontinuous coefficient G0.
Similar analysis needs to be performed before using the second-order
LW-method. The issues here are related to balancing the effects of
numerical dispersion, numerical diffusion and large artificial source
terms,
with the regularization of G0 and with the source
term  .
.
In this
project the PI plans to investigate
the effects that need to be taken into account when hyperbolic
equations with discontinuous coefficients and singular source terms are
simulated in order to obtain
the physically reasonable solutions.
Error analysis will be performed by generalizing the ideas presented in
[10] to the
systems with
discontinuous coefficients.
3. Schedule
Although the development of a general existence and uniqueness
theory for quasilinear hyperbolic problems with
discontinuous coefficients is one of the goals of the PI's research,
it is unrealistic to expect that within the two years of the duration
of this
grant the PI and the students will be able to complete the
theory. A realistic goal is to study equations
(1) and (2)
and gain an insight into the properties
of the solutions that can be generalized to a larger class of
equations.
D.
Institutional
commitment and sources of
additional support
The PI has external support which expires this summer. A renewal for the grant will be submitted in the Fall. If awarded, the grant will provide partial travel support and partial summer salary.
E.
Student
involvement and training opportunities
in science and engineering